Uniform vector on sphere given rotation anglesBy Paul BourkeOctober 2020
The following is a quick note on the random rotation of a vector in 3D such that the distribution on the surface of a sphere is uniform. The coordinate system for this document is right handed as shown below, we will start with a vector along the z axis and wish to find rotation angles and axes that give the uniform distribution on the sphere of the resulting vector. 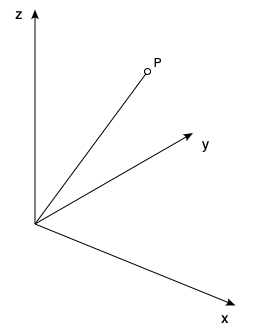
A naive way may be to imagine just choosing three angles, one for each axis and each ranging from 0 to 2π. However this leads to a higher density of points along the equator. 
One might then realise that rotating by all three axes is not necessary, one can cover the sphere with just a rotation about 2 axes. For example, a rotation about the x axis by a uniformly distributed random angle between 0 and pi, and a rotation about the z axis by a uniformly distributed random angle from 0 to 2π However, this leads to a higher density of point at the two poles. 
The solution is to modify the first rotation about the x axis, specifically as follows, where u is uniform random distribution on the range 0 to 1. 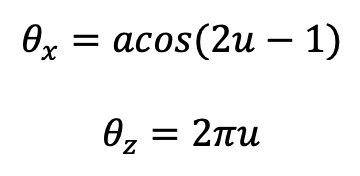

|