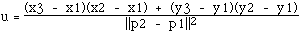Points, lines, and planesIn what follows are various notes and algorithms dealing with points, lines, and planes.
Minimum Distance between
Written by Paul Bourke |
|
| . . . 1 |
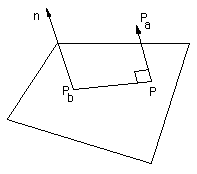
To derive this result consider the projection of the line (Pa - Pb) onto the normal of the plane n, that is just ||Pa - Pb|| cos(theta), where theta is the angle between (Pa - Pb) and the normal n. This projection is the minimum distance of Pa to the plane.
This can be written in terms of the dot product as
That is
|
| . . . 2 |
Since point (xb, yb, zb) is a point on the plane
|
| . . . 3 |
Substituting equation 3 into equation 2 gives the result shown in equation 1.
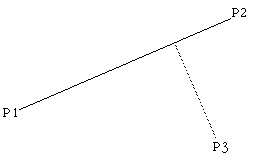
Intersection point of two line segments in 2 dimensions
Written by Paul BourkeApril 1989
This note describes the technique and algorithm for determining the intersection point of two lines (or line segments) in 2 dimensions.
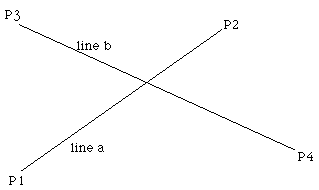
The equations of the lines are
Pb = P3 + ub ( P4 - P3 )
Solving for the point where Pa = Pb gives the following two equations in two unknowns (ua and ub)
and
Solving gives the following expressions for ua and ub
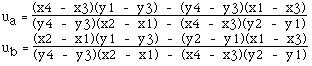
Substituting either of these into the corresponding equation for the line gives the intersection point. For example the intersection point (x,y) is
y = y1 + ua (y2 - y1)
- The denominators for the equations for ua and ub are the same.
- If the denominator for the equations for ua and ub
is 0 then the two lines are parallel.
- If the denominator and numerator for the equations for ua and ub
are 0 then the two lines are coincident.
- The equations apply to lines, if the intersection of line segments is required then it is only necessary to test if ua and ub lie between 0 and 1. Whichever one lies within that range then the corresponding line segment contains the intersection point. If both lie within the range of 0 to 1 then the intersection point is within both line segments.
Source code contributions
Original C code by Paul Bourke.
Python version by Yuangan Zhou.
C++ contribution by Damian Coventry.
LISP implementation by Paul Reiners.
C version for Rockbox firmware by Karl Kurbjun.
C# version by Olaf Rabbachin.
VB.net version by Olaf Rabbachin.
VBA implementation by Giuseppe Iaria.
Javascript version by Leo Bottaro.
The shortest line between two lines in 3D
Written by Paul BourkeApril 1998
Two lines in 3 dimensions generally don't intersect at a point, they may be parallel (no intersections) or they may be coincident (infinite intersections) but most often only their projection onto a plane intersect.. When they don't exactly intersect at a point they can be connected by a line segment, the shortest line segment is unique and is often considered to be their intersection in 3D.
|
The following will show how to compute this shortest line segment that joins two lines in 3D, it will as a bi-product identify parallel lines. In what follows a line will be defined by two points lying on it, a point on line "a" defined by points P1 and P2 has an equation. similarly a point on a second line "b" defined by points P4 and P4 will be written as
The values of mua and mub range from negative to positive infinity. The line segments between P1 P2 and P3 P4 have their corresponding mu between 0 and 1. |
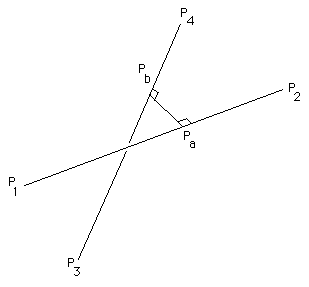
|
There are two approaches to finding the shortest line segment between lines "a" and "b". The first is to write down the length of the line segment joining the two lines and then find the minimum. That is, minimise the following
Substituting the equations of the lines gives
The above can then be expanded out in the (x,y,z) components. There are conditions to be met at the minimum, the derivative with respect to mua and mub must be zero. Note: it is easy to convince oneself that the above function only has one minima and no other minima or maxima. These two equations can then be solved for mua and mub, the actual intersection points found by substituting the values of mu into the original equations of the line.
An alternative approach but one that gives the exact same equations is to realise that the shortest line segment between the two lines will be perpendicular to the two lines. This allows us to write two equations for the dot product as
(Pa - Pb) dot (P4 - P3) = 0
Expanding these given the equation of the lines
( P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ) dot (P4 - P3) = 0
Expanding these in terms of the coordinates (x,y,z) is a nightmare but the result is as follows
d1343 + mua d4321 - mub d4343 = 0
where
Note that dmnop = dopmn
Finally, solving for mua gives
and back-substituting gives mub
Source code contributions
Original C source code from the author: lineline.c
Contribution by Dan Wills in MEL (Maya Embedded Language): source.mel.
A Matlab version by Cristian Dima: linelineintersect.m.
A Maxscript function by Chris Johnson: LineLineIntersect.ms
LISP version for AutoCAD (and Intellicad) by Andrew Bennett: int1.lsp and int2.lsp
A contribution by Bruce Vaughan in the form of a Python script for the SDS/2 design software: L3D.py
C# version by Ronald Holthuizen: calclineline.cs
VBA VB6 version by Thomas Ludewig: vbavb6.txt
LabView implementation by John van Schaijk: V01_LineLine3D.vi.zip
Luau version by Fraser: ShortestLine3D.lua
Intersection of a plane and a line
Written by Paul BourkeAugust 1991
Contribution by Bryan Hanson: Implementation in R
and Graham Wise: C#
This note will illustrate the algorithm for finding the intersection of a line and a plane using two possible formulations for a plane.
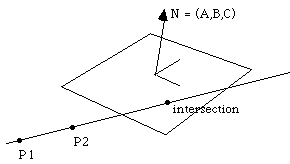
Solution 1
The equation of a plane (points P are on the plane with normal N and point P3 on the plane) can be written as
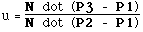
- If the
denominator is 0 then the normal to the plane is perpendicular to the
line. Thus the line is either parallel to the plane and there are no solutions
or the line is on the plane in which case there are an infinite number of
solutions
- If it is
necessary to determine the intersection of the line segment between
P1 and P2 then just check that u is between 0 and 1.
Solution 2
A plane can also be represented by the equation
Substituting in the equation of the line through points P1 (x1,y1,z1) and P2 (x2,y2,z2)
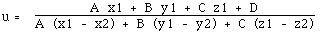
- the denominator is 0 then the normal to the plane is perpendicular to the
line. Thus the line is either parallel to the plane and there are no solutions
or the line is on the plane in which case are infinite solutions
- if it is necessary to determine the intersection of the line segment between P1 and P2 then just check that u is between 0 and 1.
Equation of a plane
Written by Paul BourkeMarch 1989
|
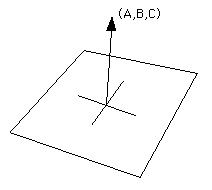
The standard equation of a plane in 3 space is
The normal to the plane is the vector (A,B,C). |
|
Given three points in space (x1,y1,z1), (x2,y2,z2), (x3,y3,z3) the equation of the plane through these points is given by the following determinants.
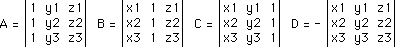
Expanding the above gives
A = y1 (z2 - z3) + y2 (z3 - z1) + y3
(z1 - z2)
B = z1 (x2 - x3) + z2 (x3 - x1) + z3
(x1 - x2)
C = x1 (y2 - y3) + x2 (y3 - y1) + x3
(y1 - y2)
- D = x1
(y2 z3 - y3 z2) +
x2 (y3 z1 - y1 z3) +
x3 (y1 z2 - y2 z1)
Note that if the points are collinear then the normal (A,B,C) as calculated above will be (0,0,0).
The sign of s = Ax + By + Cz + D determines which side the point (x,y,z) lies with respect to the plane. If s > 0 then the point lies on the same side as the normal (A,B,C). If s < 0 then it lies on the opposite side, if s = 0 then the point (x,y,z) lies on the plane.
AlternativelyIf vector N is the normal to the plane then all points p on the plane satisfy the following
N . p = k
where . is the dot product between the two vectors.
ie: a . b = (ax,ay,az) . (bx,by,bz) = ax bx + ay by + az bz
Given any point a on the plane
N . (p - a) = 0
The intersection of two planes
Written by Paul BourkeFebruary 2000
Define the two planes with normals N as
N2 . p = d2
The equation of the line can be written as
Where "*" is the cross product, "." is the dot product, and u is the parameter of the line.
Taking the dot product of the above with each normal gives two equations with unknowns c1 and c2.
N2 . p = d2 = c1 N1 . N2 + c2 N2 . N2
Solving for c1 and c2
c2 = ( d2 N1 . N1 - d1 N1 . N2) / determinant
determinant = ( N1 . N1 ) ( N2 . N2 ) - ( N1 . N2 )2
Note that a test should first be performed to check that the planes aren't parallel or coincident (also parallel), this is most easily achieved by checking that the cross product of the two normals isn't zero. The planes are parallel if
Intersection of three planes
Written by Paul BourkeOctober 2001
A contribution by Bruce Vaughan in the form of a Python script for the SDS/2 design software: P3D.py.
The intersection of three planes is either a point, a line, or there is no intersection (any two of the planes are parallel).
The three planes can be written as
N2 . p = d2
N3 . p = d3
In the above and what follows, "." signifies the dot product and "*" is the cross product. The intersection point P is given by:
| d1 ( N2 * N3 ) + d2 ( N3 * N1 ) + d3 ( N1 * N2 ) | |
| P = | ------------------------------------------------------------------------- |
| N1 . ( N2 * N3 ) |
The denominator is zero if N2 * N3 = 0, in other words the planes are parallel. Or if N1 is a linear combination of N2 and N3.
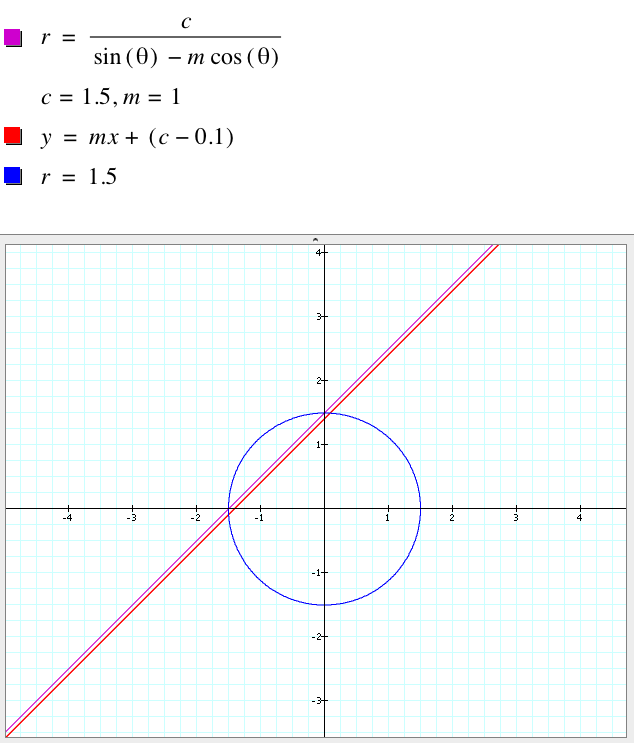
Equation of a line in polar coordinates
Written by Paul BourkeMarch 2013
How might one represent a line in polar coordinates?
In Cartesian coordinates it can be represented as:
The derivation is quite straightforward once one realises that for a point (r, theta) the x axis is simply r cos(theta) and the y axis is r sin(theta). Substituting those into the equation for the line gives the following result.
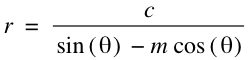
Example from the Graphing Calculator.
Question
Given a line defined by two points L1 L2, a point P1 and angle z (bearing from north) find the intersection point between the direction vector from P1 to the line.
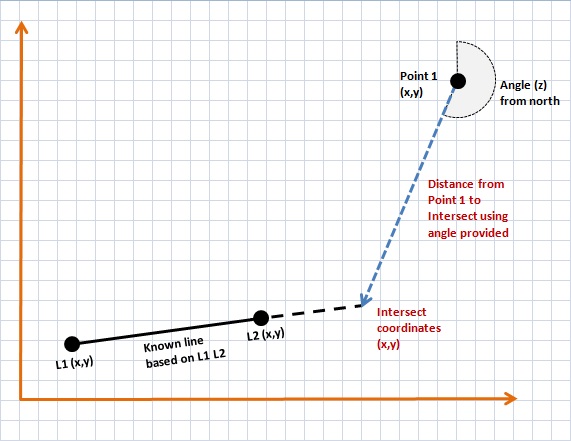
Short answer: choose a second point P2 along the direction vector from P1, say P2 = (xP1+sin(z),yP1+cos(z)). Apply the algorthm here for the intersection of two line segments. Perform the additional test that ub must be greater than 0, the solution where ub is less than 0 is the solution in the direction z+180 degrees.