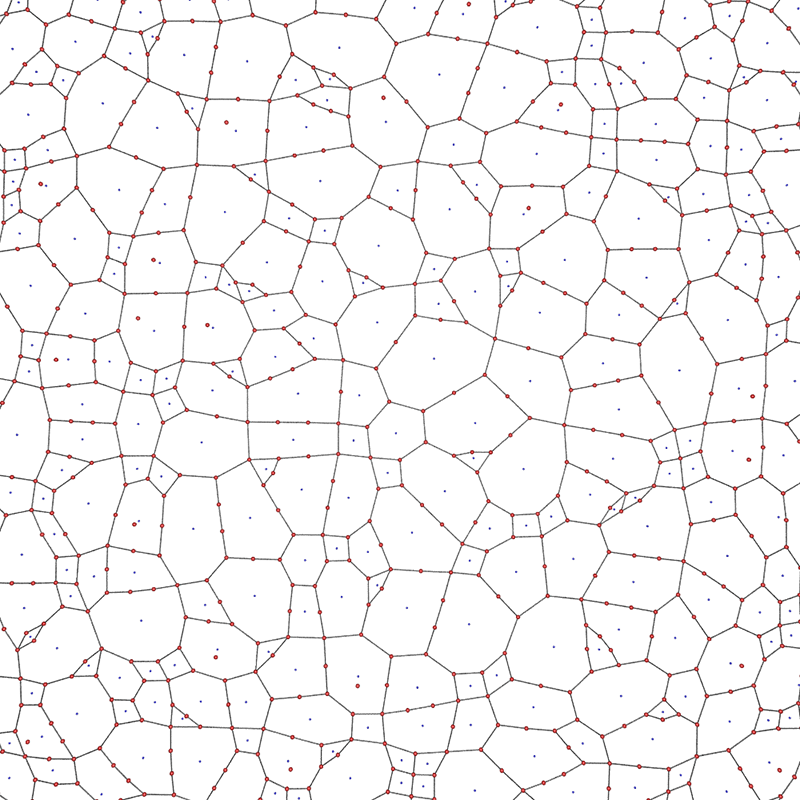
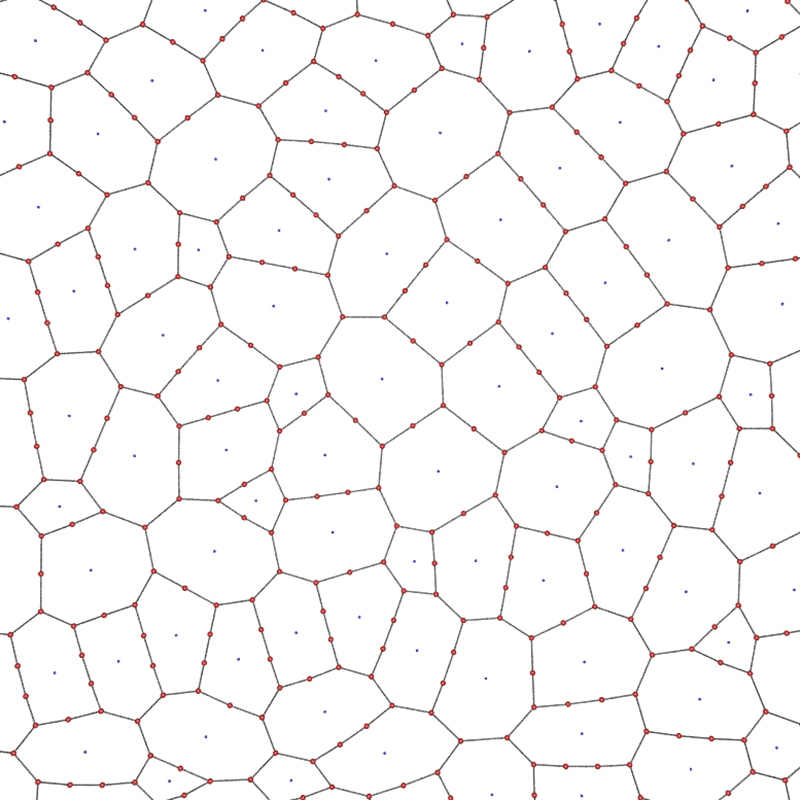
Polygonal tilingsWritten by Paul BourkeJuly 2015
The following presents polygonal tilings created for simulations requiring partitions of a surface for research into connectivity in brain science. They are presented here separately to document the way they were achieved which may be applicable to other areas, and because they seem to give natural looking formations. The basic algorithm outline starts with a regular connectivity of either a triangular, square, or hexagonal (others are possible) mesh. These are represented as nodes, edges in terms of node ids, and polygons as list of edge ids. A user specified number of edges are randomly removed, this of course generates polygons with a higher number of boundary edges. The user may specify a maximum number of allowed polygon edges, additionally some polygon lengths may be explicitly excluded. For example in the original application pentagons were not allowed. The resulting mesh network is allowed to relax under the physical system where nodes are modelled as electrically charged points (they repelled each other) and edges are modelled as springs which both repelled or attracted depending on the rest length of the spring. The result is a network where edge lengths attempt to be constant length and nodes attempt to be evenly separated (avoiding crossovers that would otherwise occur). The three starting mesh types are presented below along with two frames, one immediately after the edges are removed and one after the relaxation. In all these 3 cases only 500 edges are removed and the removal is such that polygon lengths will not exceed 10 edges. Note that in the case of hexagons, the double height odd column offset arrangement for the initial conditions is equivalent in the connectivity sense to the more traditionally laid out hexagonal mesh.
It should be noted that not all possible polygon lengths are possible. For example, starting with squares initially one can never form any polygon without first forming hexagons (by removing one shared edge). Starting with hexagons one can only initially create 10 sided polygons. Other such limitations on desired polygon length distributions will be left up to the reader to consider. There are a number of other issues that can arise from the straightforward random deletion of edges. One of many examples is shown below, starting with a square grid and removing random edges one can end up with so called "dangling edges", that is, edges not Associated in a meaningful way with any polygon. In the current implementation these are deleted after the edge removal stage, they could equally be precluded in the edge remove stage. 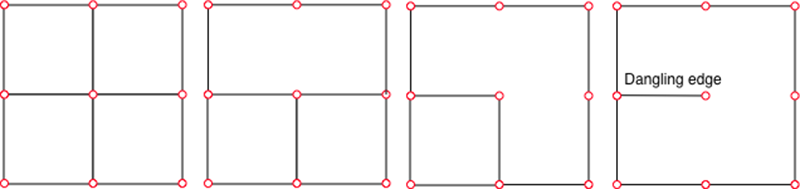
Further examples
Various examples are provided below varying the starting grid topology, the number of deleted edges, and the maximum allowed polygon edge length. In the cases indicated by "exhaustive edges removed", this indicates where edges are removed until no more can be removed due to the maximum allowed polygon edge length.  Square mesh start, maximum of 16 edge polygons, 1000 edges removed.
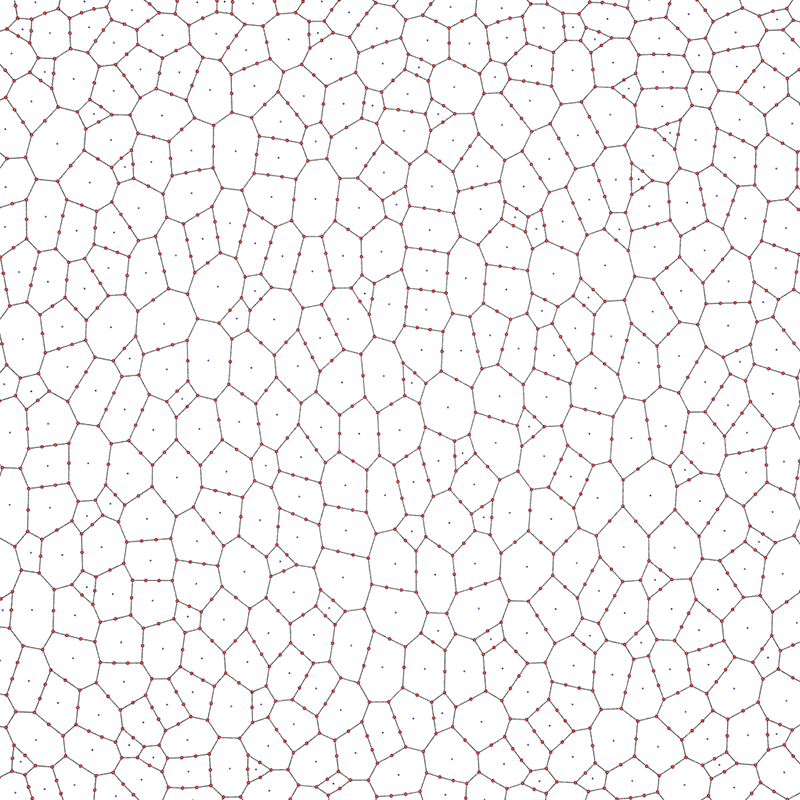 Hexagonal mesh start, maximum of 10 edge polygons, exhaustive edges removed.
 Triangular mesh start, maximum of 10 edge polygons, 2000 edges removed.
 Relaxed version of the above topology.
 Triangular mesh start, maximum of 6 edge polygons, exhaustive edges removed.
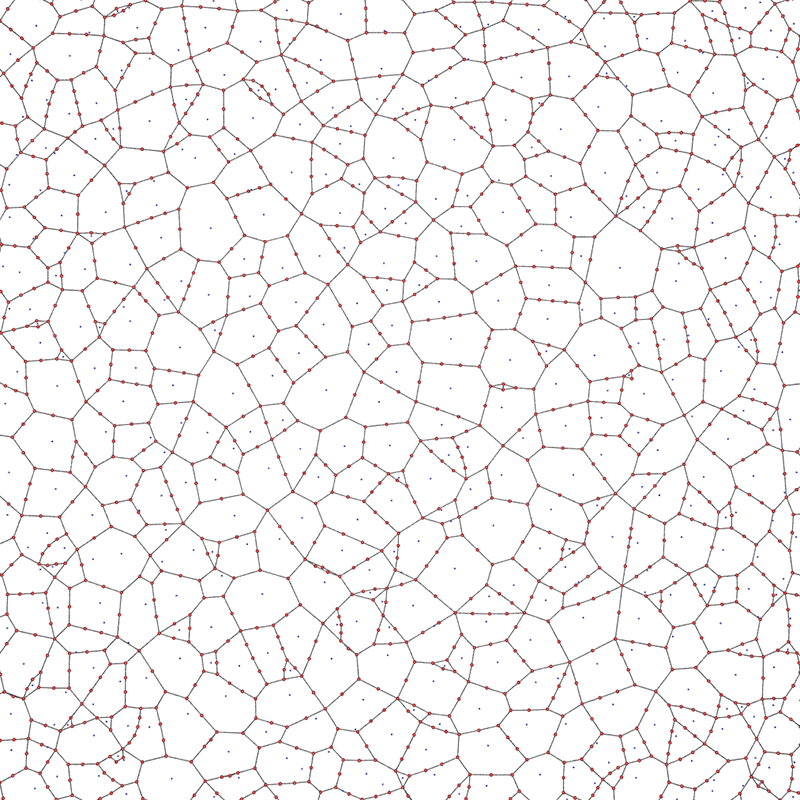 Triangular mesh start, maximum of 12 edge polygons, exhaustive edges removed.
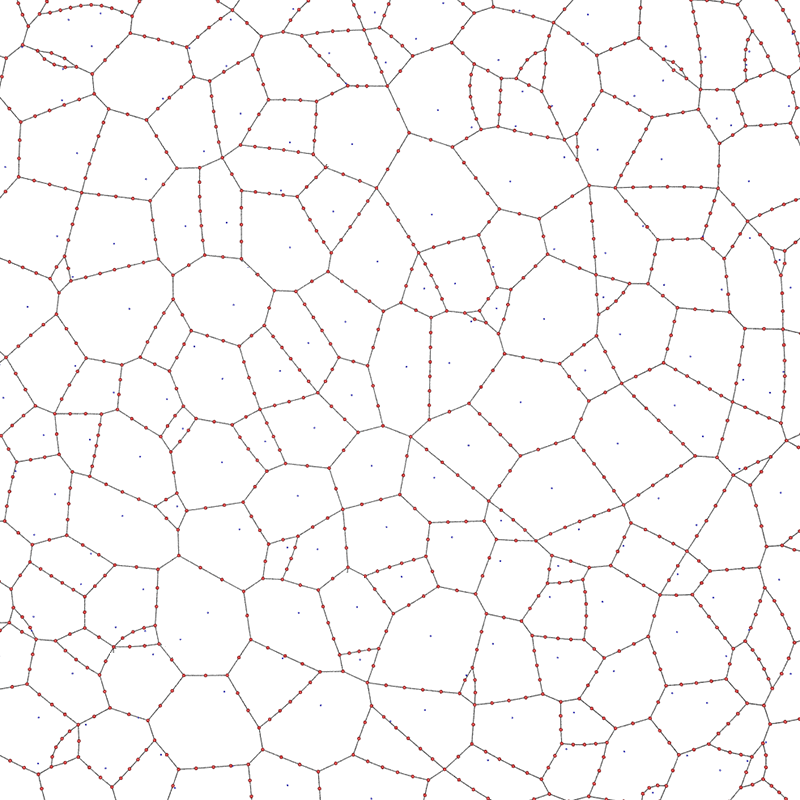 Triangular mesh start, maximum of 24 edge polygons, exhaustive edges removed.
 Triangular mesh start, maximum of 4 edge polygons, exhaustive edges removed.


|