Implicit surfaces

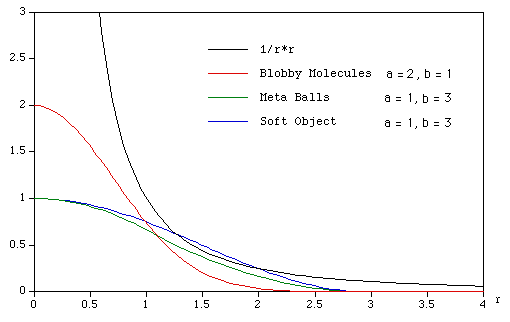
Introduction

Most computer based 3D geometric modelling is done with basic primitives such as lines, planes, boxes, etc. Many smooth and deformable objects are difficult or inefficient to represent with such building blocks, even if primitives such as spheres or Bezier/spline surfaces are used. An increasingly popular approach has been the use of field functions in 3D, the surfaces being isosurfaces through the field.

The following summarises three common methods for creating so called "implicit surfaces". That is, surfaces which are contours (isosurfaces) through some scalar field in 3D. There are three commonly used techniques each distinguished by their field functions. The field function determines the value at every point in space due to some underlying primitive geometric objects, normally points, line segments, and polygonally bounded planes.

Consider the field function D(r) = 1/r² and a number of control points in 3D space. r is the distance of a point in space to a particular control point. The total field strength at any point in space is the sum of the field strengths due to each control point. A contour can be drawn through this space resulting in a 3D surface.

For example if there is a single control point different colour levels will result in spheres of different radius. If there are two control points the combined fields will interact, the resulting isosurface will bulge between the two control points depending on their relative distance apart. This is shown below for a range of control point distances.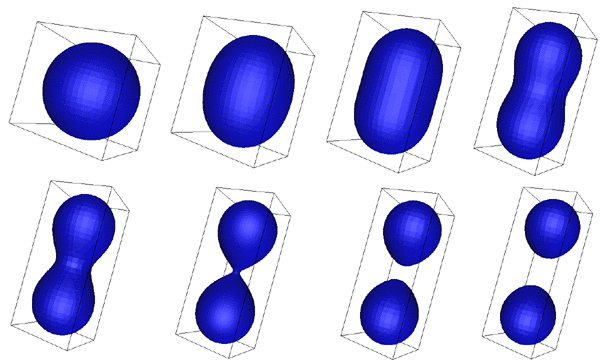

If the control structure is a line or a plane then the distance r is normally taken to be the closest distance to nay point on the line or plane. The following shows lines along the axis with varying field strength.

One problem with line primitive is their interaction at junctions. A straightforward implementation will result in a bulge at the intersection of two line segments. In the following there are two line primitives approaching each other, the blend together as expected but in the image at the bottom where they touch, a bulge results. This is often (not always) an undesirable feature, normally one would expect two touching line segments to behave as one. There are blending functions which overcome this, alternatively the lines can be shortened by an amount which depends on the type of field functions being used.

Blobby Molecules

Perhaps the earlier widely used field function is attributed to Jim Blinn and modelled after electron density fields.

"b" is related to the standard deviation of the curve, "a" to the height. The function should be recognised as a Gaussian curve centered at the origin, actually a half Gaussian as r >= 0.

Meta Balls

One of the problems with the first example and blobby molecules is the field function extends to infinity, that is, to calculate the field at a point in space requires a summation of the contribution from each of the control primitives. This becomes computationally expensive as the number of control primitives increases. The next two field functions are bounded, after some distance from a control primitive they don't contribute to the field strength.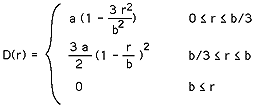

"a" is a scaling factor, "b" is the maximum distance a control primitive contributes to the field.

Soft Objects

This field function is attributed to work by the Wyvill brothers, it is basically the first few terms in a series expansion of an exponential truncated to restrict the range of influence.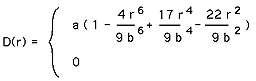

"a" scales the function, each control primitive has no influence after a distance "b". This function has a slight advantage over that for Meta balls as it only uses squares of the distance and so it isn't necessary to compute square roots.

Notes

• A comparison of the different field functions is illustrated in the following graph.

  

• The functions described here guarantee a continuous and smoothly changing surface.

• These surfaces can be easily and smoothly morphed and deformed by slowly changing the attributes of the control primitives.

• The question as to whether points are on the interior or exterior of the surface is implicit to the description.

• Geometric primitives don't need to only add to the field, making "a" in the above formula negative will turn that primitive into a subtractive contributor.

• Implicit surfaces can most readily be viewed in traditional rendering packages by polygonisation with for example the marching cubes algorithm. Alternatively various researchers are written raytracers that trace implicit surfaces directly.

People have known for a long time that if you have two implicit surfaces f(x,y,z)=0 and g(x,y,z)=0 that are fairly continuous, with a common sign convention (f and g positive on the inside, negative on the outside, say) then the implicit surface defined by f+g=0 is a blend of the shapes.

The van der Waals surfaces of molecules (roughly speaking, iso-potentials of the electron density) are described in Chemistry and Physics books and [Max 1983]. To create animation of DNA for Carl Sagan's COSMOS TV Series, Jim Blinn proposed approximating each atom by a Gaussian potential, and using superposition of these potentials to define a surface. He ray traced these and called them "blobby models".

Shortly thereafter, people at Osaka University and at Toyo Links in Japan began using blobby models also. They called theirs "metaballs" (or, when misspelled, "meatballs"). Yoichiro Kawaguchi became a big user of their software and their Links parallel processor machine to create his "Growth" animations which have appeared in the SIGGRAPH film show over the years. The graduate students implementing the metaball software under Koichi Omura at Osaka used a piecewise quadratic approximation to the Gaussian, however, for faster ray-surface intersection testing (no need for iterative root finders; you just solve a quadratic).

Bloomenthal has discussed techniques for modelling organic forms (trees, leaves, arms) using blobby techniques (though he prefers the term "implicit modelling") and for polygonizing these using adaptive, surface-tracking octrees. The latter algorithm is not limited to blobby models, but works for any implicit model, not just blobs. Polygonization allows fast z-buffer renderers to be used instead of ray tracers, for interactive previewing of shapes. A less general variant of this algorithm was described in the "marching cubes" paper by Lorensen and some bugs in this paper have been discussed in the scientific visualization community in the years since. In the sci-vis community, people call them "iso-surfaces" not "implicit surfaces".

Meanwhile, in Canada and New Zealand, the Wyvill brothers, and grad students, were doing investigating many of the same ideas: approximations of Gaussians, animation, and other ideas. Rather than "blobbies" or "metaballs", they called their creations "soft objects". But it's really the same idea.

References

Nelson L. Max
Computer Representation of Molecular Surfaces
IEEE Computer Graphics and Applications, Aug 1983

James F. Blinn
A Generalization of Algebraic Surface Drawing
ACM Transactions on Graphics, July 1982

Jules Bloomenthal
Polygonization of Implicit Surfaces
Computer Aided Geometric Design, Issue 5, 1988

Brian Wyvill, Craig McPheeters, Geoff Wyvill
Animating Soft Objects
The Visual Computer, Issue 4 1986

Brian Wyvill, Craig McPheeters, Geoff Wyvill
Soft Objects
Advanced Computer Graphics (Proc. CG Tokyo 1986)

Brian Wyvill, Geoff Wyvill
Field Functions for Implicit Surfaces
Visual Computer, Issue 5 1989

Fujita, T., Hirota, K. and Murakami, K
Representation of Splashing Water using Metaball Model
Fujitsu, 1990, Vol 41, part 2, pp 159-165

Tatsumi, H., Takaoki, E., Omura, K. and Fujito, H.
A new method for 3D reconstruction from serial sections by computer graphics using meta-balls: reconstruction of "Hepatoskeletal System" formed by Ito Cells in the Cod Liver
Computers and Biomedical Research, 1990

Chanderjit Bajaj and I. Ihm
C1 Smoothing of Polyhedra with Implicit Algebraic Splines
SIGGRAPH 1992

Chanderjit Bajaj
Surface Fitting with Implicit Algebraic Surface Patches
Topics in Surface Modelling, ed. by H. Hagen, SIAM Publications, 1992

Payne, B. A. and Toga, A. W
Distance Field Manipulation of Surface Models
IEEE Computer Graphics and Applications, January 1992

Graves, G.
The Magic of metaballs"
Computer Graphics World, May 1993

Hart, J.
Ray Tracing Implicit Surfaces<
Siggraph 93 Course Notes No 25