DürehedronWritten by Paul BourkeOctober 2020
See also: Movies showing a range of cutting distances
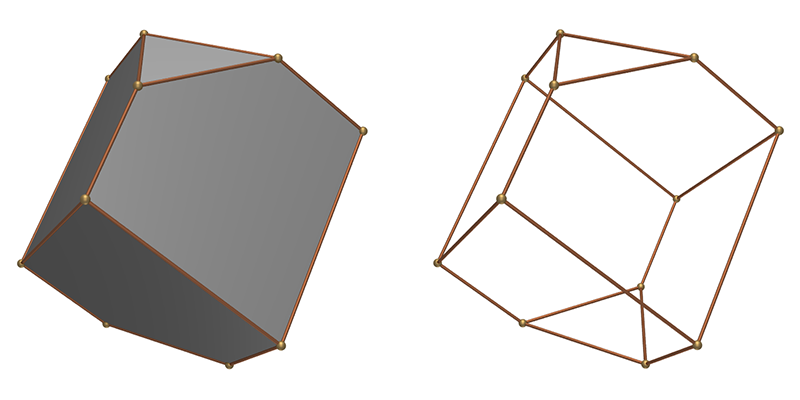
I will define the dürehedron here as a specific configuration of a more general 3D polyhedra created as the bounding volume between 6 angled planes and a further two planes performing a cut at the top and bottom. The 6 angled planes are two in groups, an upper and lower group, the lower group being the mirror image of the upper group and rotated by 60 degrees. Each of the groups consist of three planes orientated at some angle to the vertical (typically around 30 degrees) and rotated about the vertical axis by intervals of 120 degrees. The result is a solid with 6 five sided "kite-like" faces (rhombi) and two triangular faces, one at each of the vertical extreme. The dürehedron can be characterised by two values, the cutoff height and the angle of the inclined planes to the vertical. The two poles shown along the vertical are determined by where the inclined planes intersect. 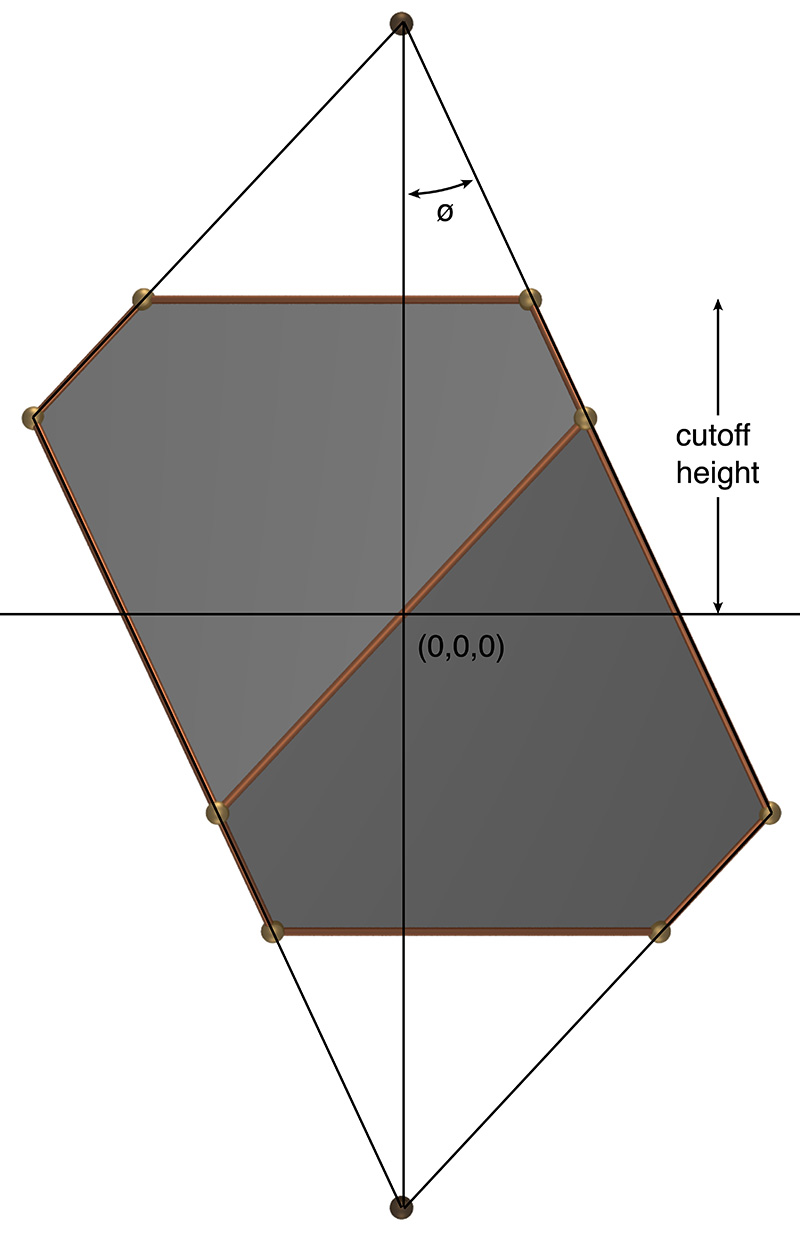 The two defining parameters, one angle and length
Also variously known as a truncated triangular trapezohedron or truncated rhombohedron. The general form is representative of a calcite crystal. Also referred by a Joachim Camerarius, a contemporary, of Dürer as a quadratum saxum. An interesting feature of the solid is that irrespective of the values of cut distance and tilt angle, the sum of the internal angles of the 5 sided faces is always 540 degrees. The top and bottom caps are, from symmetry, equilateral triangles with internal angles of 60 degrees. 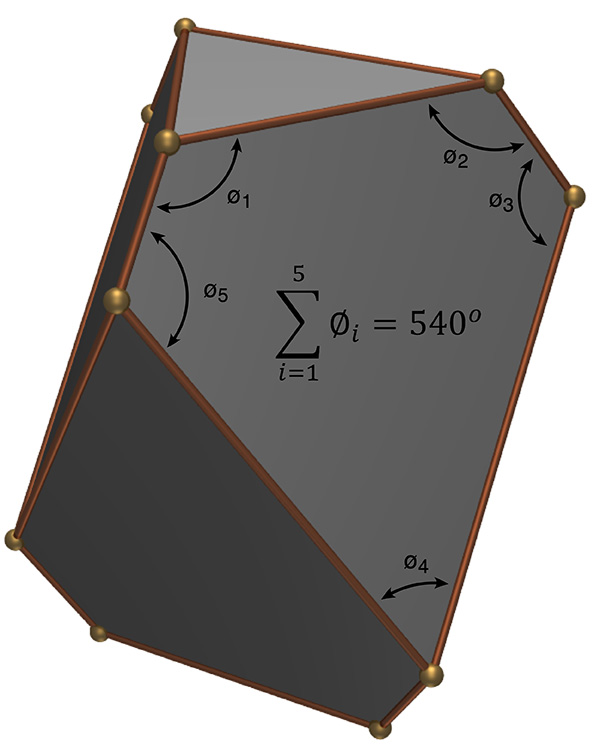 Sum of the internal angles of the 5 sided faces is always 540 degrees.
Historically Dürers solid (1471-1528) is from the representation in an engraving by Albrecht Dürer titled Melancholia I., hence the use of his name in the naming of the more general shape here. The exact proportions of the solid in the engraving is not documented, neither is it obvious.  Engraving named Melancholia I by Albrecht Dürer
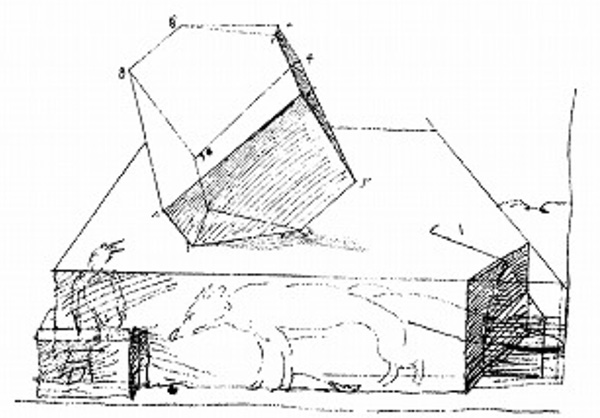 Preliminary sketch by Albrecht Dürer
In trying to determine the exact proportions of this early engraving researchers have focused on the angle of the acute corner of the rhombus. Various suggestions have been proposed, the most common being one of 54, 60, 72, 80 and even 90 degrees. In the case of 90 degrees the shape degenerates to a cube truncated by planes perpendicular to the long diagonal, certainly the simplest explanation. While the solid in the engraving does not appear cubic, it has been suggested that it has simply been stretched in the vertical axis. That is, a trigonal trapezohedron truncated by planes perpendicular to the long axis. 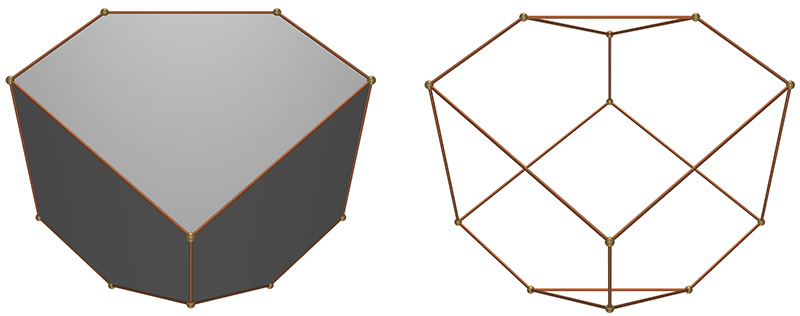 90 degree angle at acute rhombus corner, plane angle 35.26 degrees
Note that only specifying the angle at the acute rhombus corner does not uniquely define the solid, another parameter is needed to define the height of the top and bottom cutting plane. Some researchers have used the height from the acute angle of the rhombus to the midpoint of the opposite edge as this second parameter. An acute rhombus angle of 54 degrees is quoted by some as special, and a characteristic of the "philosophers stone". In this case the other rhombus angles are 126 and 117 degrees exactly. 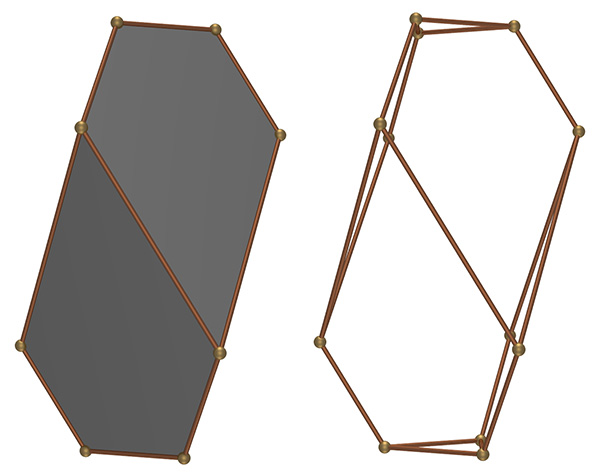 54 degree angle at acute rhombus corner, plane angle 17.1 degrees
There is another special case when the acute angle is 72 degrees, the other rhombus angles are 108 and 126 degrees exactly. 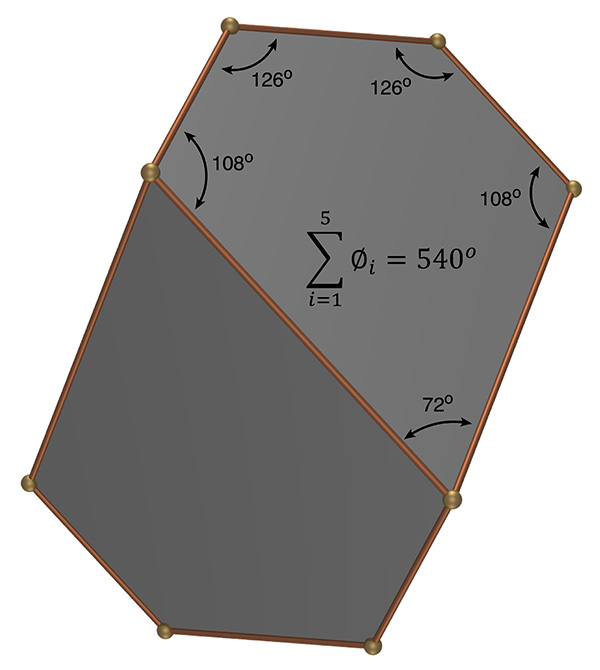 Special case of 72 degree acute angle, plane angle 24.8 degrees
It has been proposed by some that the solid in the etching has all the vertices lying on the surface of a sphere. This is not a unique situation and one example is illustrated below with a cutting height of 0.811 and plane angle of 23.774 degrees.  Vertices lying on surface of a sphere
Addendum
The following is the internal face and vertex numbering scheme used in the generation software developed during the creation of this document. 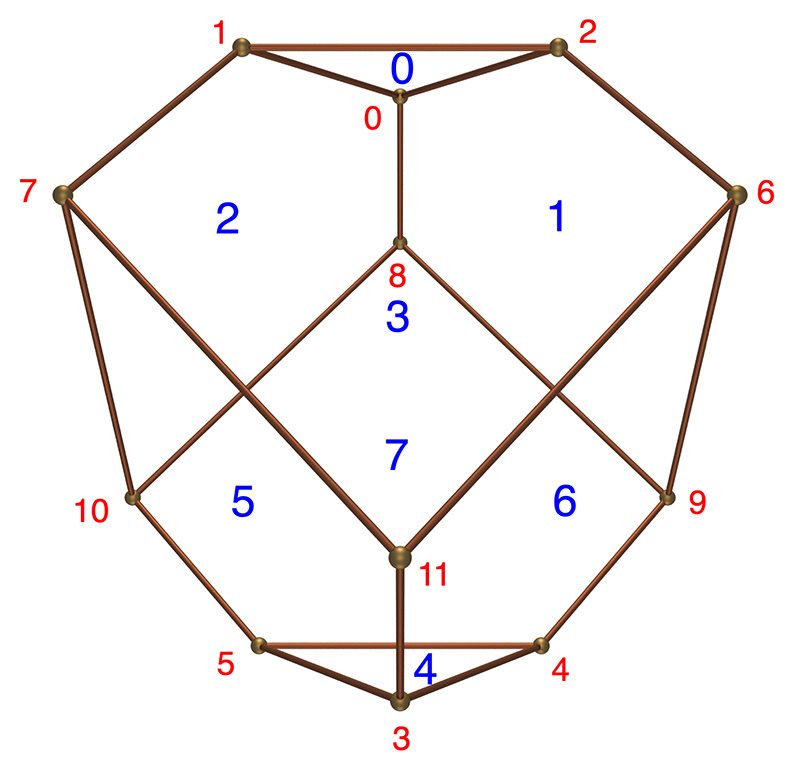 Vertex and face numbering conventions.
|