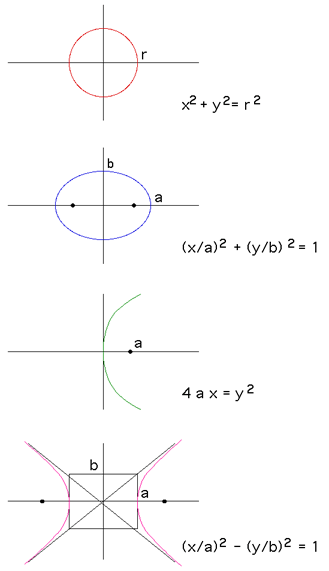Conic SectionsWritten by Paul BourkeJune 2002
If a cylinder is sliced by a plane a number of curves arise depending on the angle of the plane with respect to the cylinder axis, these are called conic sections. Conic sections were studied extensively by the Greeks as early as 350 BC in an attempt to solve the great geometric problems of the day, namely, squaring the circle, duplicating the cube, and trisecting an angle. They were also studied extensively in relation to Keplers laws of planetary motion by Descartes and Fermat. There are four different classes of curve (circle, ellipse, parabola, and hyperbola) and they are illustrated below. 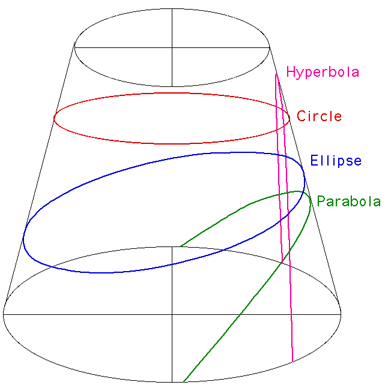
|