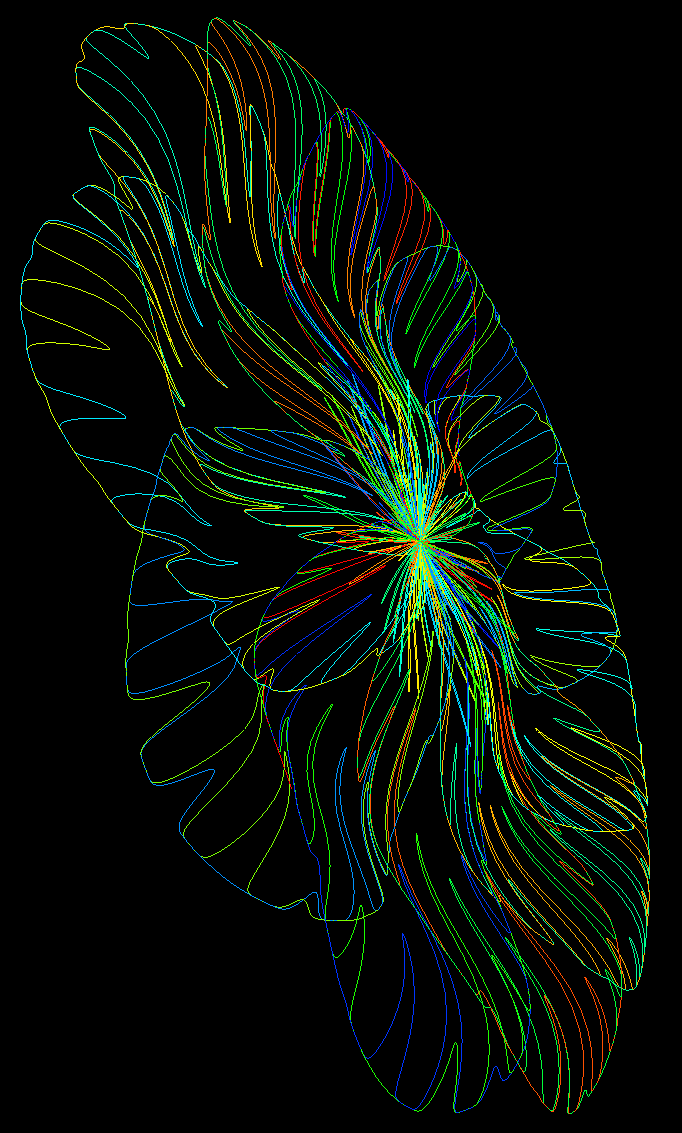
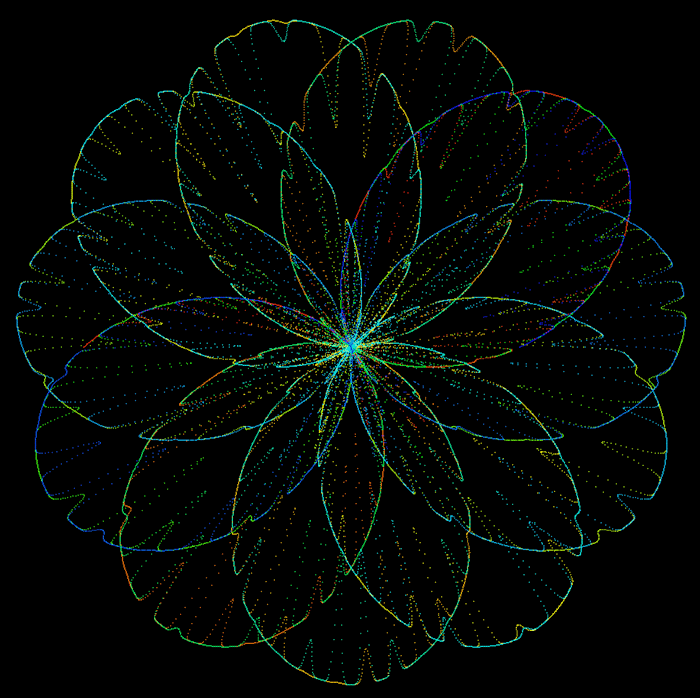
Chrysanthemum CurveWritten by Paul Bourke
Attributed to Temple Fay
The chrysanthemum curve is given in polar coordinates by the following
and in Cartesian coordinates y = r sin(u)

#include "stdlib.h"
#include "stdio.h"
#include "math.h"
typedef struct {
double x,y,z;
} XYZ;
#define N 30000
int main(int argc,char **argv)
{
int i;
double u,r,p4,p8;
XYZ p,plast;
for (i=0;i<=N;i++) {
u = i * 21.0 * PI / N;
p4 = sin(17 * u / 3);
p8 = sin(2 * cos(3 * u) - 28 * u);
r = 5*(1 + sin(11*u/5)) - 4*p4*p4*p4*p4 * p8*p8*p8*p8*p8*p8*p8*p8;
p.x = r * cos(u);
p.y = r * sin(u);
p.z = (r/20+.2)*sin(r*TWOPI/7);
if (i > 0)
--- write the line plast -> p in your favourite format ---
plast = p;
}
}
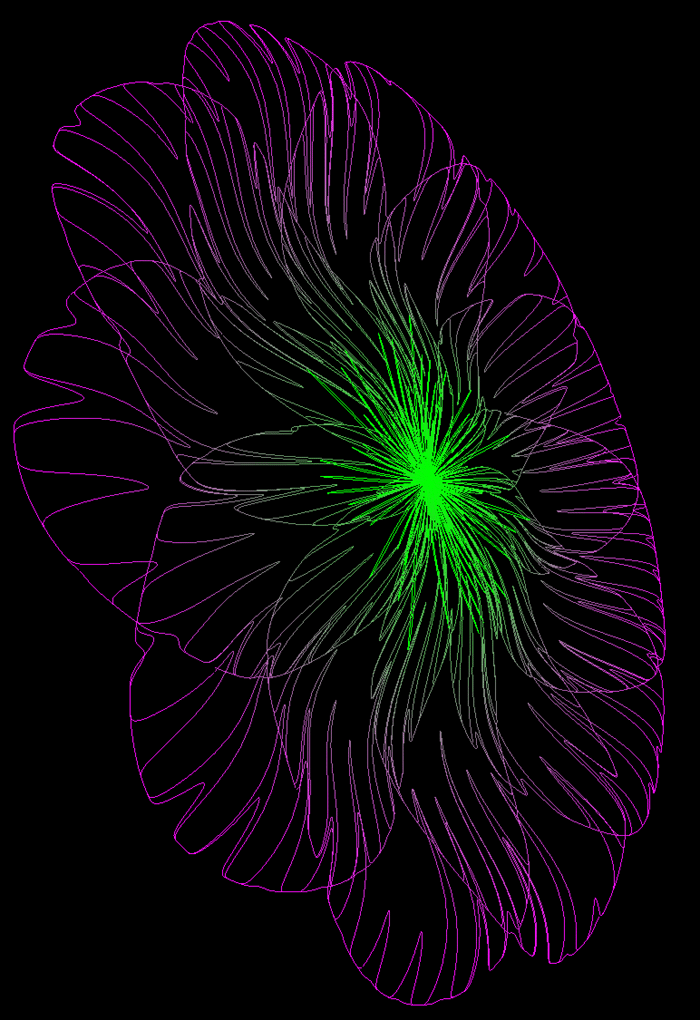
Anaglyph contribution by Jean Tousset.  [Click for higher resolution version] |