Borromean RingsWritten by Paul BourkeOctober 1997
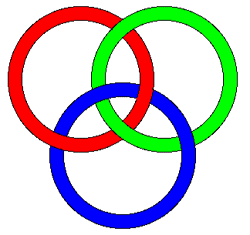
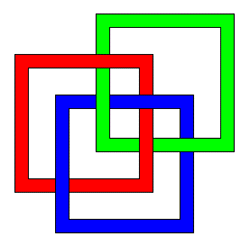
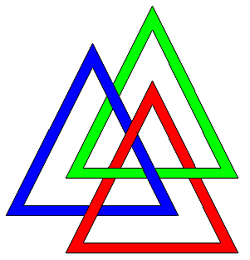
Borromean rings are three interlinked rings such that no two rings are linked. In other words, the three rings cannot be separated and yet no two of them are linked. It can be shown that there is no solution for flat rings, it can only be constructed by perturbing the rings in a third dimension. The rings can be formed with various base geometries including rectangles and triangles as shown below.
One way (as shown below) to create the rings mathematically is with the following three parametric equations, one for each ring.
(cos(u) , sin(u) + r , cos(3u) / 3)
(cos(u) + 0.5 , sin(u) - r/2 , cos(3u) / 3)
(cos(u) - 0.5 , sin(u) - r/2 , cos(3u) / 3)
Where u = 0 -> 2πi This is illustrated below for r = sqrt(3)/3, the radius of the spheres placed along the path is 0.2 
It is possible to make the rings out of elliptical rings, it does require 3 dimensions. The parametric equations for the three "rings" are
( 0 , r1 cos(u) , r2 sin(u) )
( r2 cos(u) , 0 , r1 sin(u) )
( r1 cos(u) , r2 sin(u) , 0 )
Where u = 0 -> 2πi This is illustrated below for r1 = 2, r2 = 1, and the radius of the tubes = 0.2 
And finally, using box geometry...

 Contribution by Robert McGrego
|