Solid angle of a pixelWritten by Paul BourkeJuly 2017
In the following the question of how much solid angle a pixel representing a projection of a 3D scene covers will be presented. Applications for this include computing the total solid angle an object in a scene covers, for example, for lighting calculations. While what follows can be extended to any projection space, for simplicity here we will consider 90 degree by 90 degree perspective projections such as generated from cube maps. Consider one face of the cube centered at the origin as shown below. Each pixel of which may be in one or another state and the aim is to find the solid angle of all pixels in a particular state. This involves counting up the solid angle of each pixel in that state. If the aim is to find the solid angle overall then this can be applied to each of the 6 cube faces. 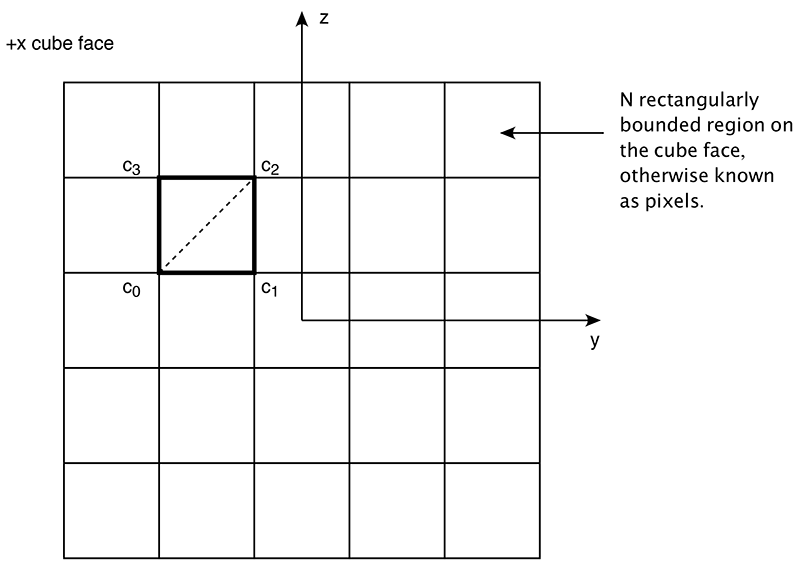
One pixel on this face of the cube is shown highlighted above, the corners labeled as shown. Consider vectors from the origin to c0 ... c3 and normalise, these are now points on a unit sphere. Splitting the 4 vertex pixel rectangle into two halves gives two spherical triangles. The shortest curve between two of these vertices are sections of a great circle (they lie on the plane that also contains the origin). The solid angle of such a triangle is simply
Where the angles Ø0 + Ø1 + Ø2 are the angles of the spherical triangle at each vertex as shown below. The tangents at each ci lie in the plane to the neighbouring point. 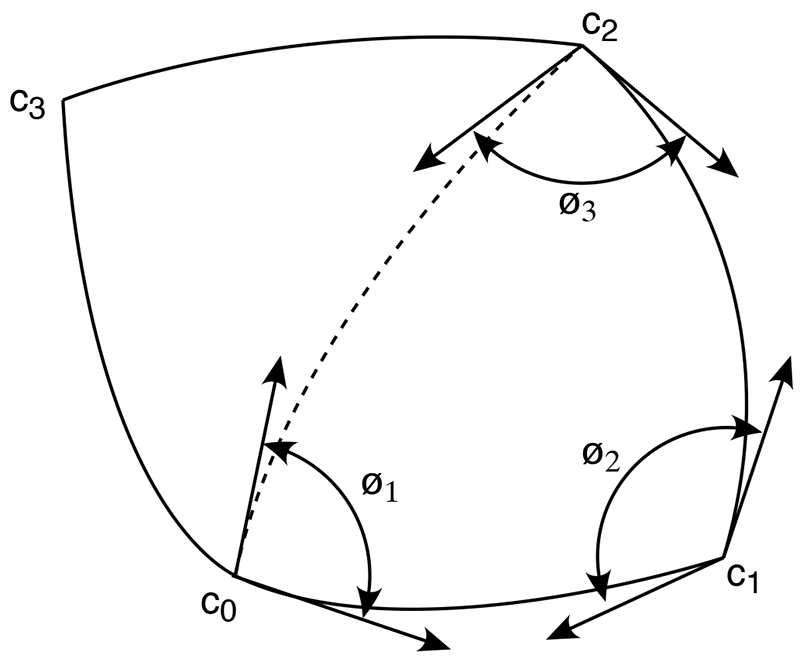
Computing the tangents at each ci is achieved using the "standard" double cross product trick. For example to find the tangent vector from c0 to c1, calculate the vector c1 - c0, take the cross product of this with the normal vector at c0 which is also c0 (sphere is at the origin). The result is a vector perpendicular to the normal at c0. The cross product of this vector with the normal at c0 is the desired tangent vector.
XYZ CalcTangent(XYZ p0,XYZ p1)
{
XYZ p,r,t;
p = VectorSub(p1,p0);
r = CrossProduct(p0,p);
t = CrossProduct(r,p0);
Normalise(&t);
return(t);
}
There are a few simple test cases for a coded implementation. If the cube face is entirely contained in the object whose solid angle is to be measured then the solid angle should be 4π/6. Consider a disk of radius R one unit from the origin. The solid angle should be 2π(1-cos(θ)) where θ is atan(R). For a bounded longitude and latitude rectangle the solid angle is given by (sin(φ2) - sin(φ1)) (θ2 - θ1) Where φ is latitude and θ longitude. |