Tetration fractalsWritten by Paul BourkeMay 2013
Addition is the repeated adding of 1 (unation). 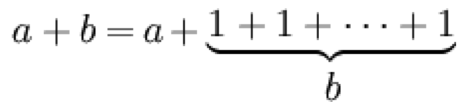
Multiplication is repeated addition (duation). 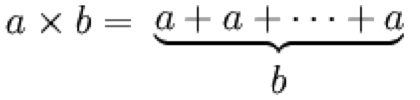
Powers or exponentiation is repeated multiplication (trination). 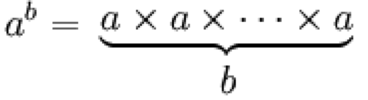
Tetration (term attributed to Reuben Louis Goodstein) is repeated exponentiation. 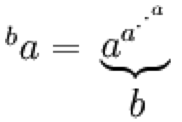
Generally for ba, "a" is referred to as the base and "b" is called the height. The notation used here is often the standard one but there are a number of other notations in common usage, many of which generalise into higher orders, pentation and beyond. As one might imagine tetration of real numbers results in really big numbers really fast as shown in the table below, the empty columns would require more space than is reasonable for all the digits. Note that by definition even0 = 1 and odd0 = 0.
But is as is often the case things get more interesting in the complex plane. In order to study the behaviour of tetration on the complex plane one needs to be able to compute the complex power of a complex number.
In the discussion here we will use the principle branch of natural logarithm of a complex number, that is, where the angle in the Euler formula is in the range of -pi to pi. Computationally this is given by the atan2() function in most programming languages. If z is written as c + id then
It should be noted that tetration is right associative and that this order is important, for example.
Implementation via a recursive function is the obvious choice noting the following definition. 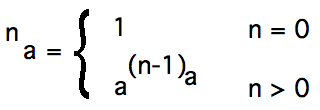
This might be implemented in C as: tetrationlibrary.h and tetrationlibrary.c Tetration behaviour that exhibits fractal characteristics (also sometimes called the "power tower fractal") can be revealed in a number of ways. One is to shade each position in the image (value "z" on the complex plane) depending on whether or not the value nz escapes to infinity as n increases. This requires a test and is similar to "bailout" parameter for typical Mandelbrot style calculations, once a term in the series exceeds this threshold value then the series is assumed to diverge to infinity. Unlike the Mandelbrot, in the tetration fractal this threshold determines the quality of the fractal, higher values are more accurate but of course take longer to compute. There are a number of possible tests, for example:
Four of the cases above are illustrated below.
 Center = (-0.5,0.0), range = 9.0
 Center = (-1.9,0.0), range = 3.0
 Center = (-0.188,0.235), range = 0.02
 Center = (-0.25,0.0), range = 0.8
 Center = (-1.3,2.85), range = 0.8
 Center = (2.2,-2.5), range = 2.0
 Center = (2.15,-0.91), range = 0.5
 Center = (-2.37,-0.38), range = 0.5
 Center = (-0.94,0.41), range = 0.2
 Center = (-0.95,2.4), range = 0.1
 Center = (0.4,2.0), range = 0.2
 Center = (-1.3,2.85), range = 0.8 References
|



