Polynomial attractorWritten by Paul BourkeSeptember 2020
I rediscovered the original article by J.C.Sprott (Sprott, J. C. "Automatic Generation of Strange Attractors." Comput. & Graphics 17, 325-332, 1993c) that was one of the inspirations for my fractal explorations. The images in that publication are rather simplistic, not a complaint but a fact of graphics in that era. I didn't readily find other example and the ones on Wolfram Mathworld were equally uninspiring. So I decided to produce some myself using my 2D histogram method along with a collection of colour maps. The attractors are based upon the equations below. yn+1 = a6 + a7xn + a8xn2 + a9xnyn + a10yn + a11yn2
 GLXOESFTTPSV
What is this "GLXOESFTTPSV"? A nice innovation in the paper was to identify the attractors by their series a0... a11. This was done by choosing values for each between -1.2 to 1.2 in steps of 0.1 and mapping those to uppercase letter A through to Y. S, GLXOESFTTPSV represents a0 = -0.6, a1 = -0.1, a2 = 1.1, a3 = 0.2, a4 = -0.8, a5 = 0.6, a6 = -0.7, a7 = 0.7, a8 = 0.7, a9 = 0.3, a10 = 0.6, a11 = 0.9.  MCRBIPOPHTBN
 VBWNBDELYHUL
 FIRCDERRPVLD
 QFFVSLMJJCCR
 LUFBBFISGJYS
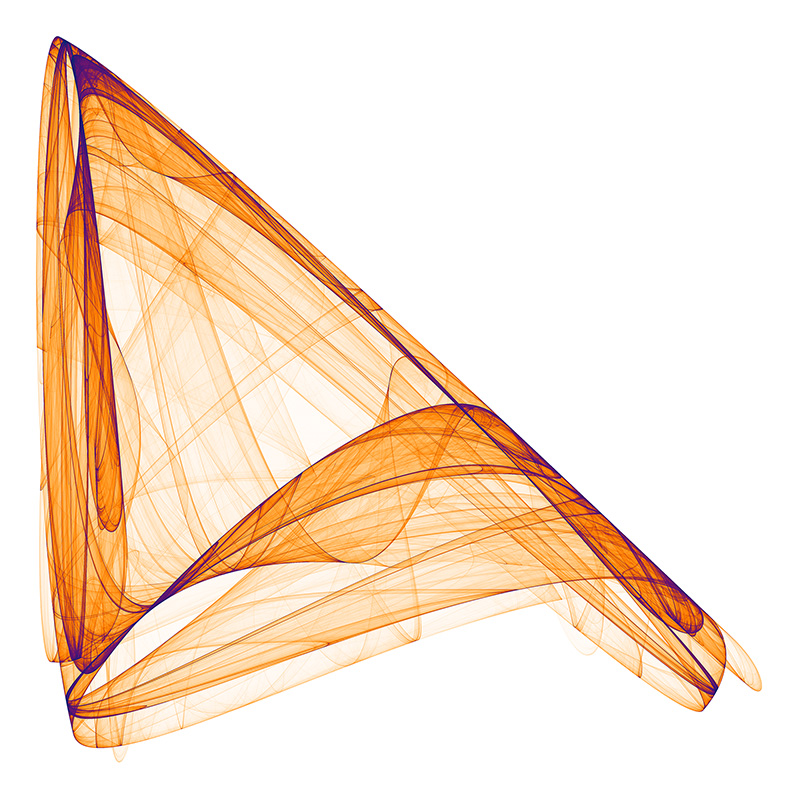 EJYDREGLYQPV
 HIYIWHOKNVCG
 MSSSRRPADDSO
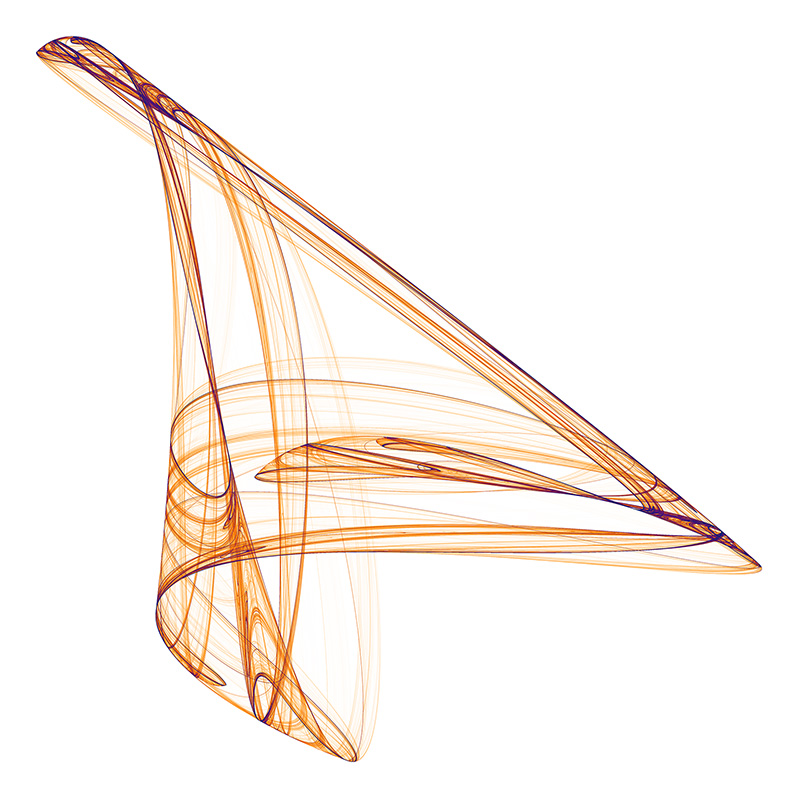 OIHVGHAHGYRK
 RALLTIOBDULT
 WJJFXGXHTRPG
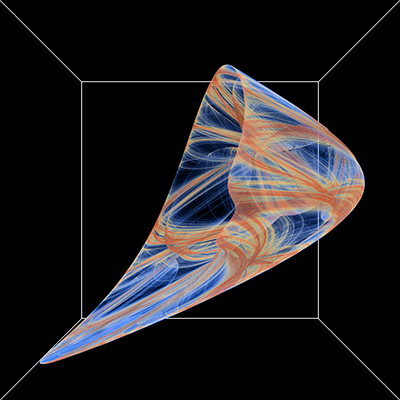
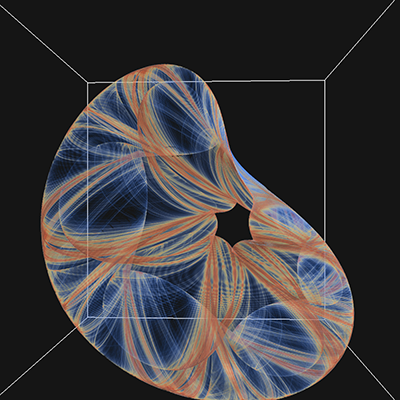
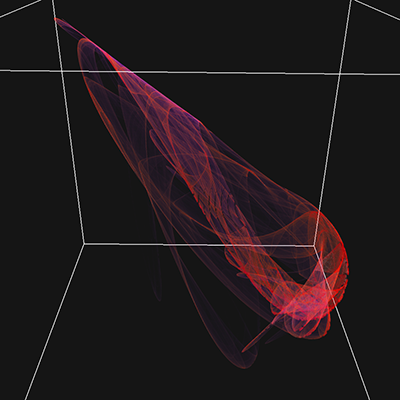
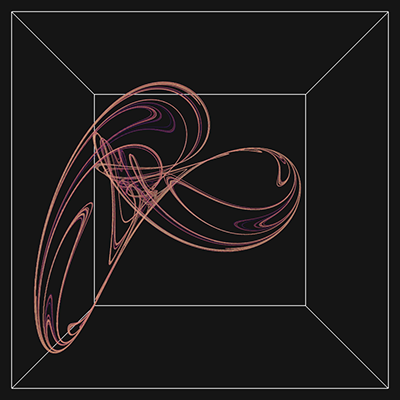
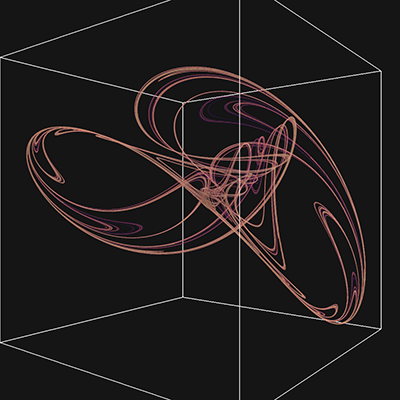
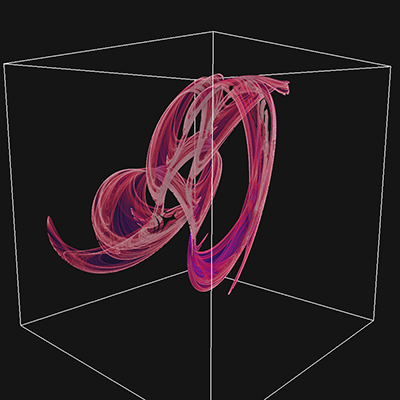
Extension to 3DThe paper extends the notion to polynomials of 3 variables (x,y,z), this results in 30 parameters for a general 2 degree polynomial. This is written here as follows, noting the convention is different to that used in a subsquent republising of the paper. yn+1 = a10 + a11xn + a12yn + a13zn + a14xn2 + a15yn2 + a16zn2 + a17xnyn + a18xnzn + a19ynzn zn+1 = a20 + a21xn + a22yn + a23zn + a24xn2 + a25yn2 + a26zn2 + a27xnyn + a28xnzn + a29ynzn
While the previous papers presented 2D projections onto a coordinate plane, here I populate a volume as a histogram and then render that volumetrically using ray casting. The volumes used in the examples here are 1000x1000x1000 voxels.
|