Multi Julia IFSWritten by Paul BourkeInspiration and equations by Chris Thomasson March 2019
Equations defining the n+1'th term of the series is 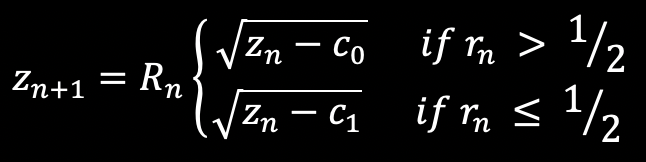
Where rn is uniform random distribution on the range of 0 to 1, and Rn is randomly either 1 or -1, with equal probabilities. In essence, rn is selecting between two constants c0 and c1, the transition of 1/2 may be varied for different effects. The Rn is choosing equally between the two roots. Some interesting values for complex valued c0 and c1 might be: c0 = {0.5,0.0}, c1 = {-5.5,0.0}c0 = {0.0,1.0}, c1 = {0.0,-1.0} c0 = {0.726514,0.240242}, c1 = {0.171039,0.235043} c0 = {-1.444991,0.139179}, c1 = {-0.063294,-1.401774} c0 = {1,0}, c1 = {-1,0} c0 = {-.75, .06 }, c1 = {-.45, .6 }


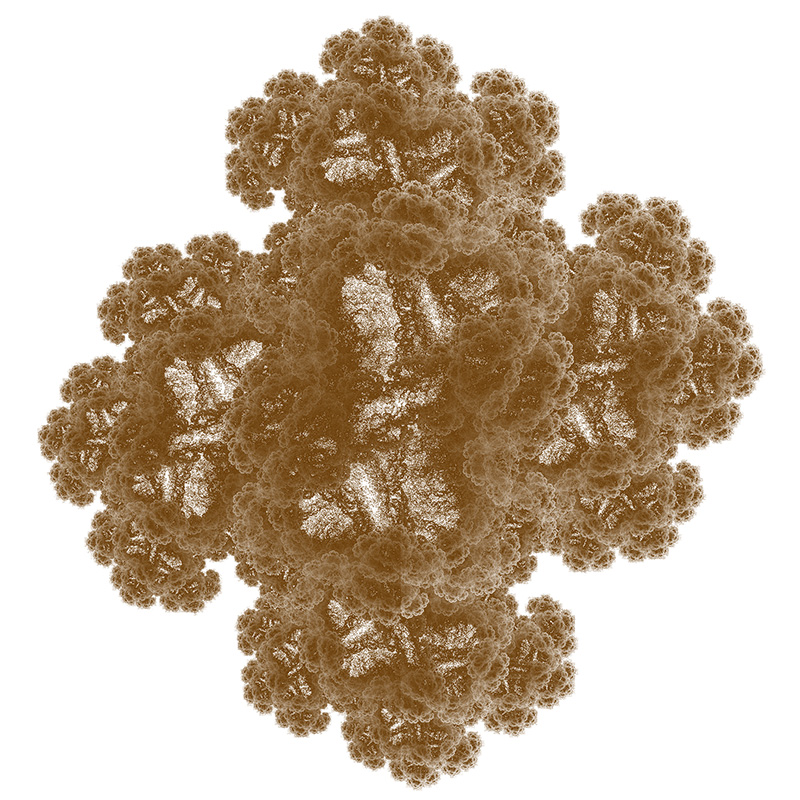
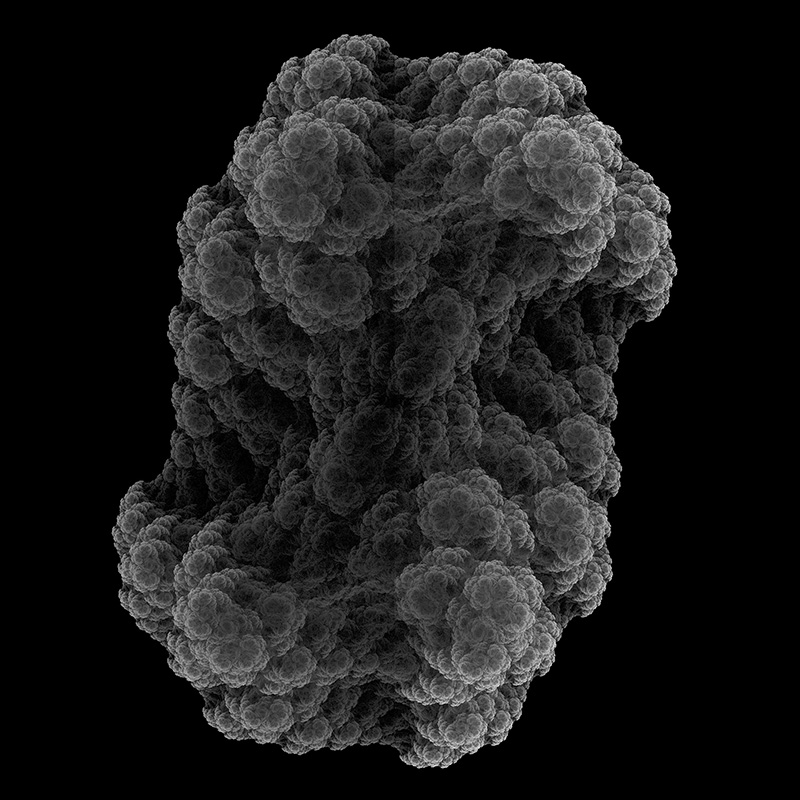


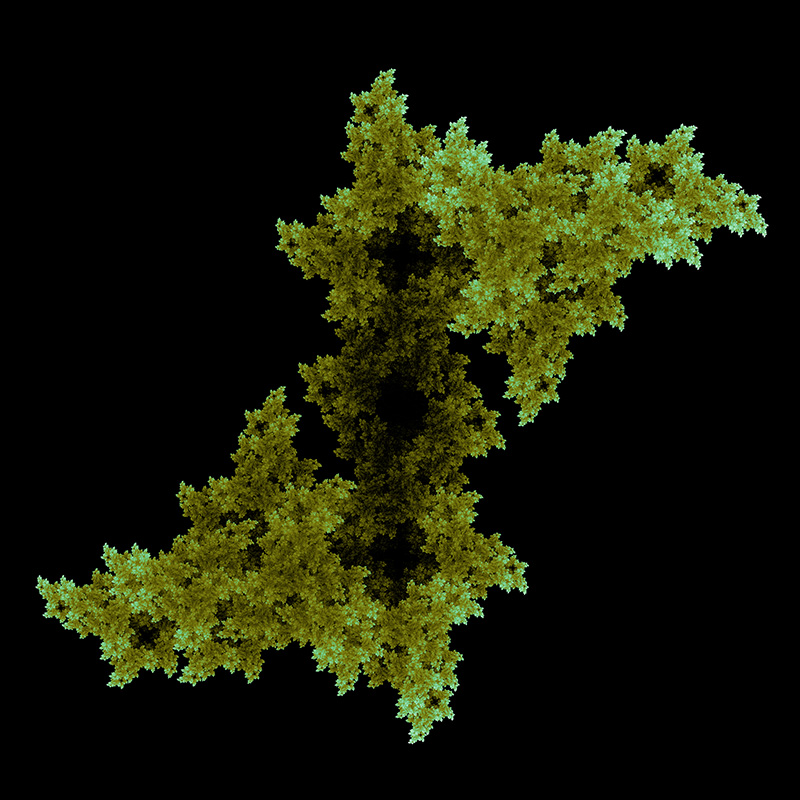
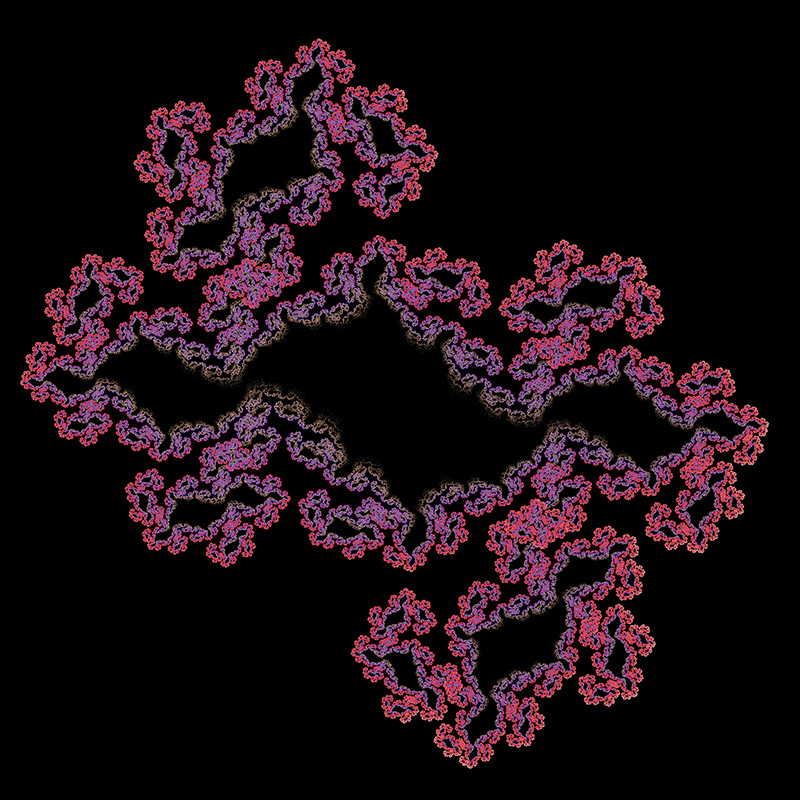
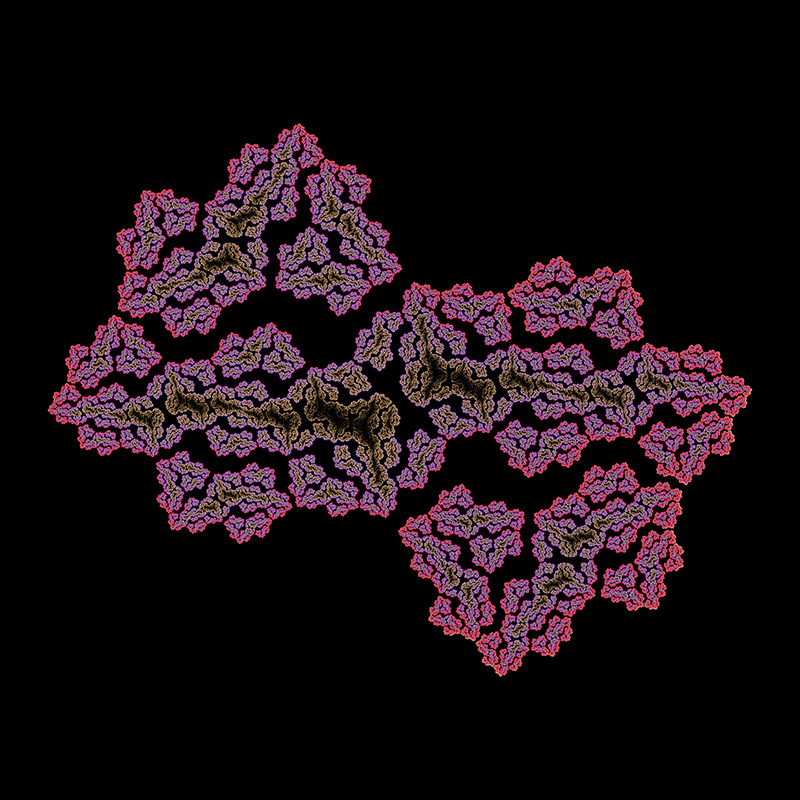

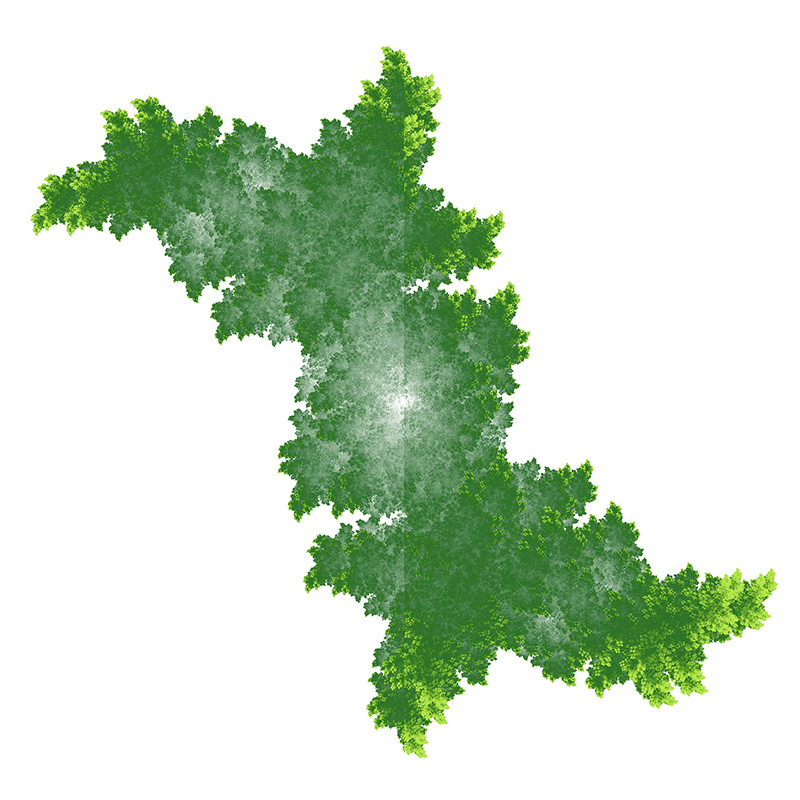

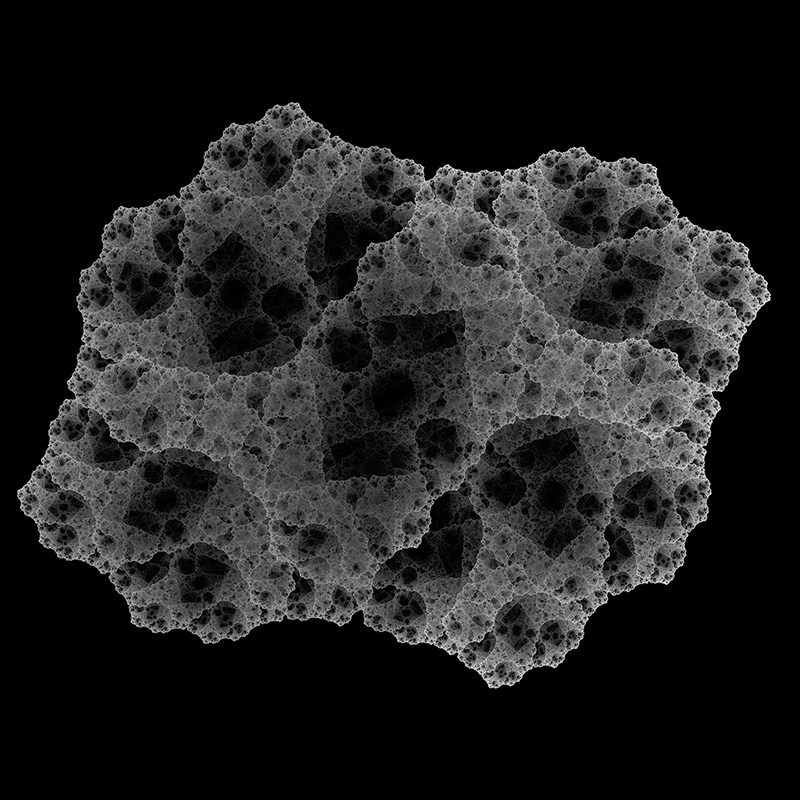





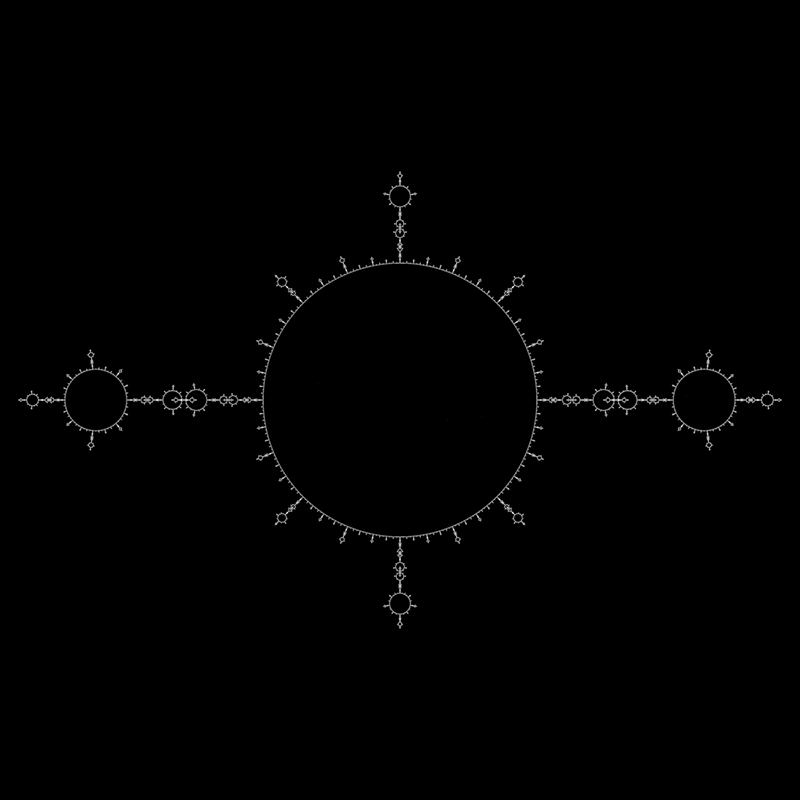


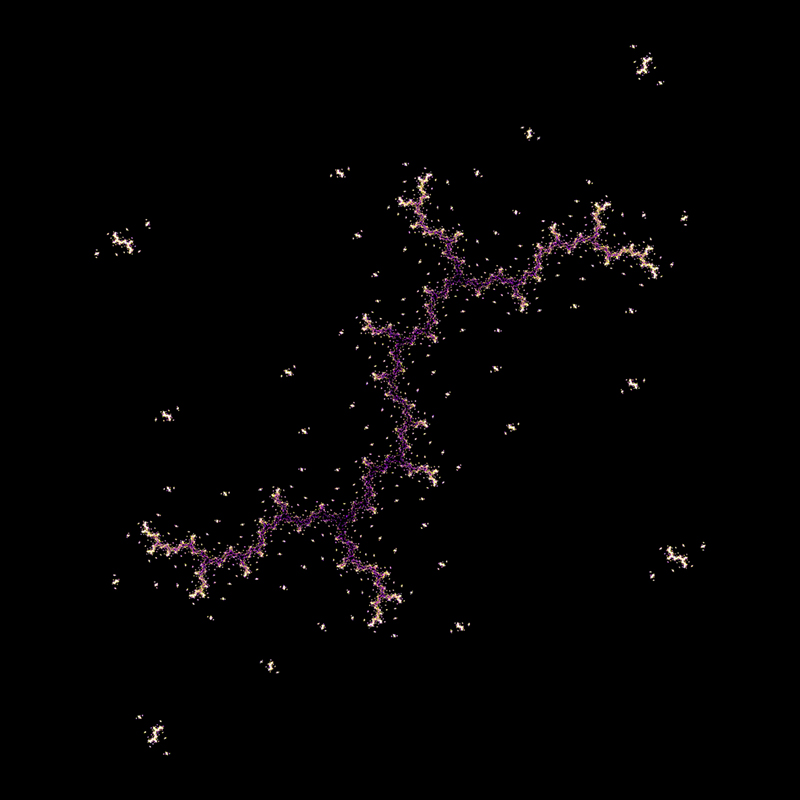
A variation, also by Chris Thomasson, uses 4 function choices instead of the 2 used above. Each chosen with equal probability.
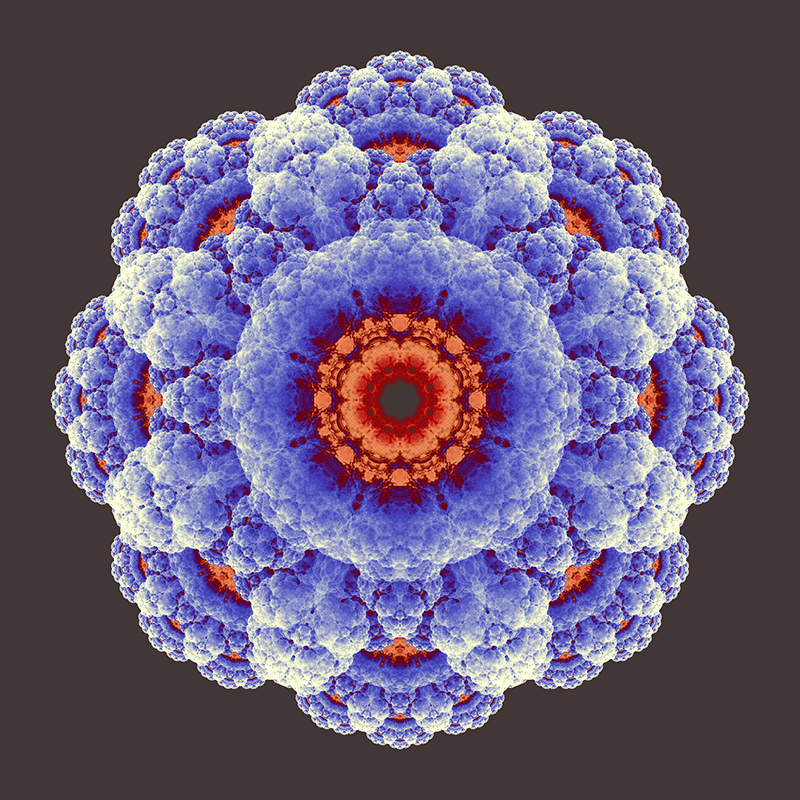

|