The Mandelbrot at a Glance

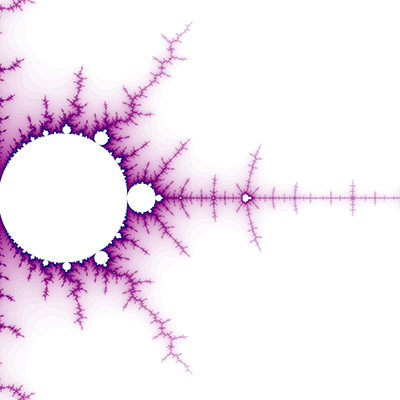
Introduction - the most well known fractal

The Mandelbrot is an image representing the behaviour of the series z_n+1 = z_n² + z₀ where z is a complex number. Each point on the complex plane sets the initial term of the series, namely z₀. If the series diverges (escapes to infinity) for a particular point z₀ then it is coloured white (or a colour or intensity related to how fast the point escaped). If the point doesn't escape the point is shaded black and is said to be inside the Mandelbrot set. The following is the entire set, in the unlikely event you haven't seen it before.

The above image is centered on (-0.75,0.0) and extends approximately 1.3 horizontally on either end, the left most point of the Mandelbrot is at (-2,0).

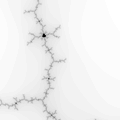
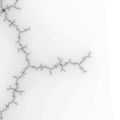
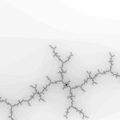
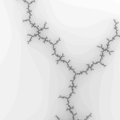
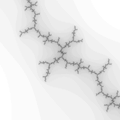
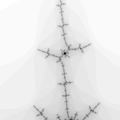
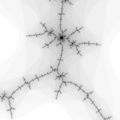
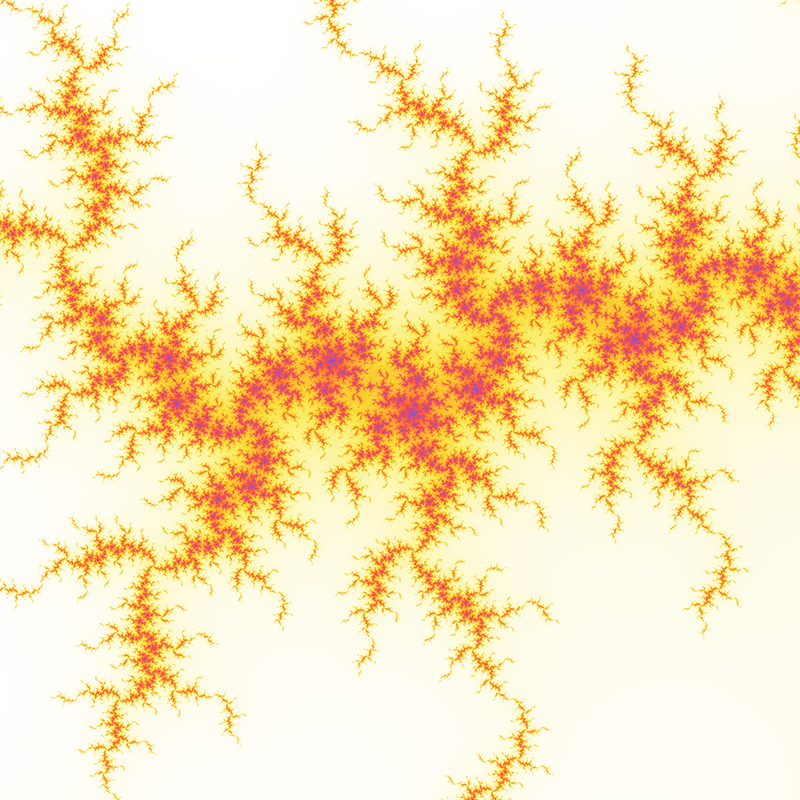
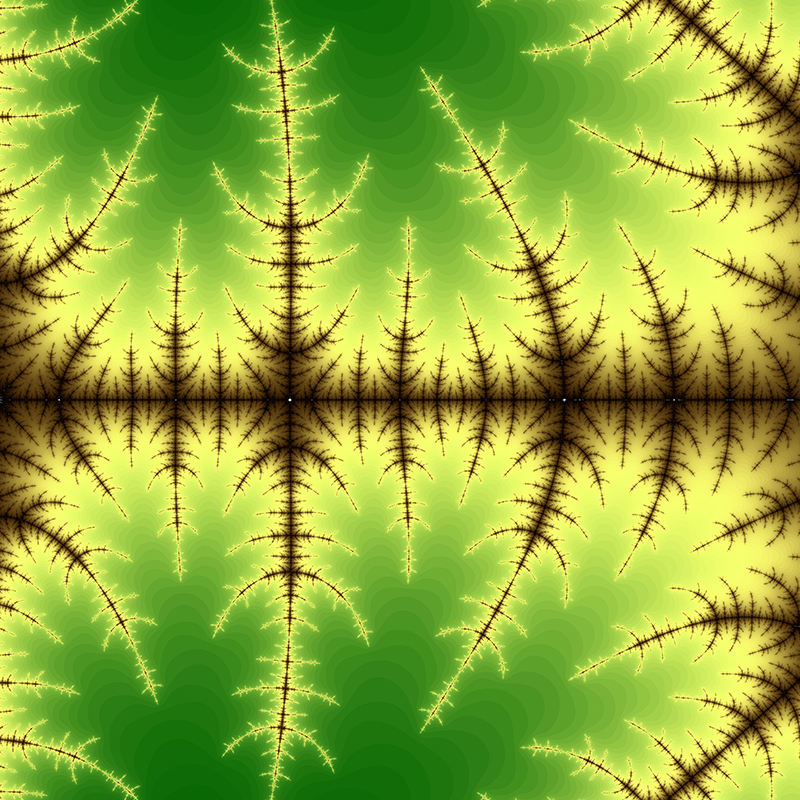
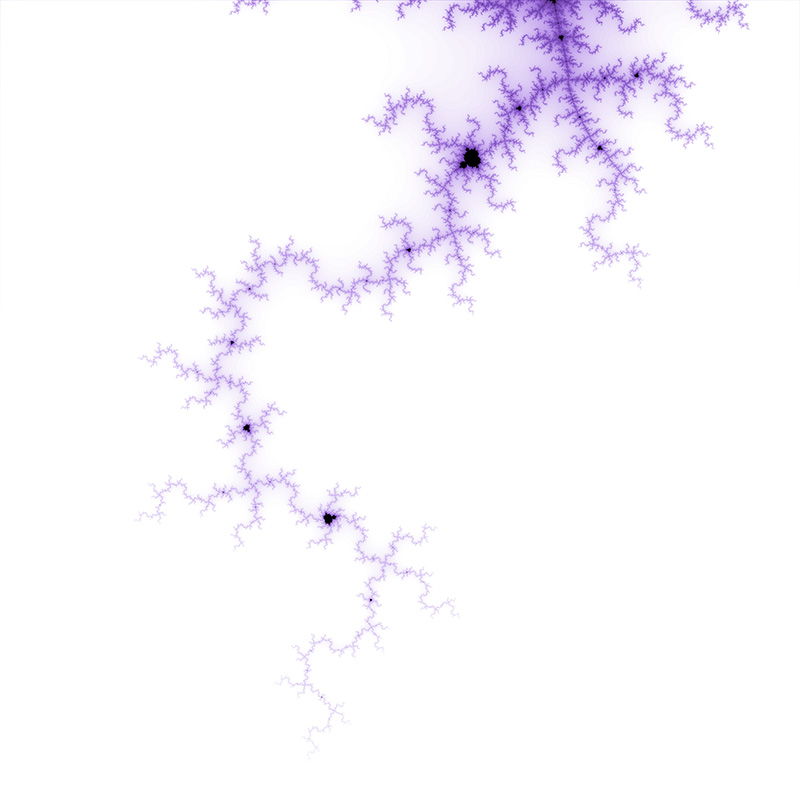
The Mandelbrot set is considered to be a single connected set. The following zoom sequence concentrates on one of the tendrils that runs from the top portion of the set. The zoom factor increases by a factor of 5 going from left to right, the zoom is about the center of each image. The center of this image on the complex plane is (-0.170337,-1.06506).

5

25

125

625

3125

15625

78125

Zoom 2

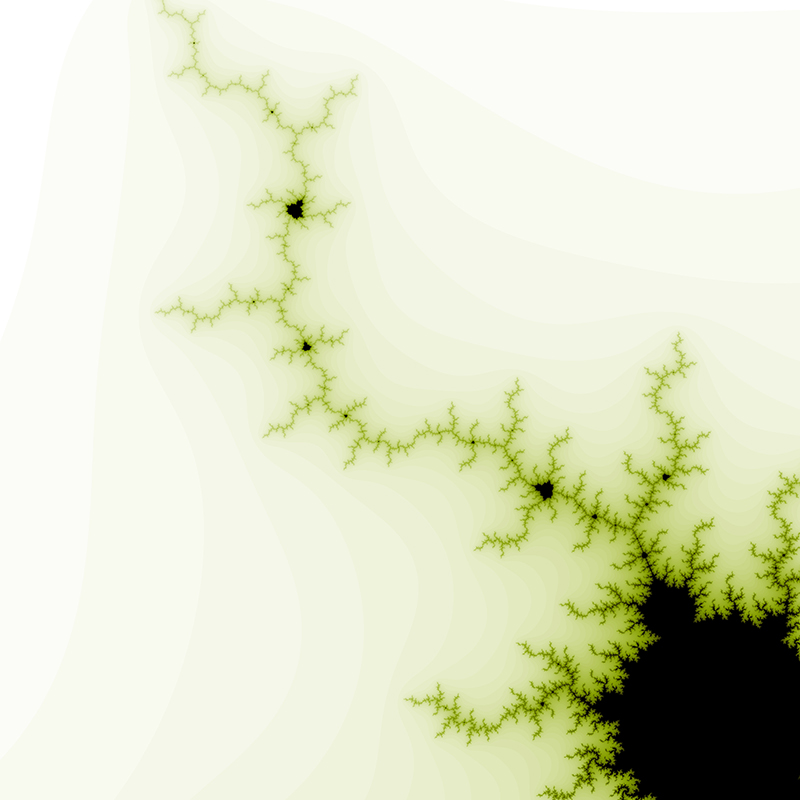
The center of this sequence is (0.42884,-0.231345).

5

25

125

625

3125

15625

78125

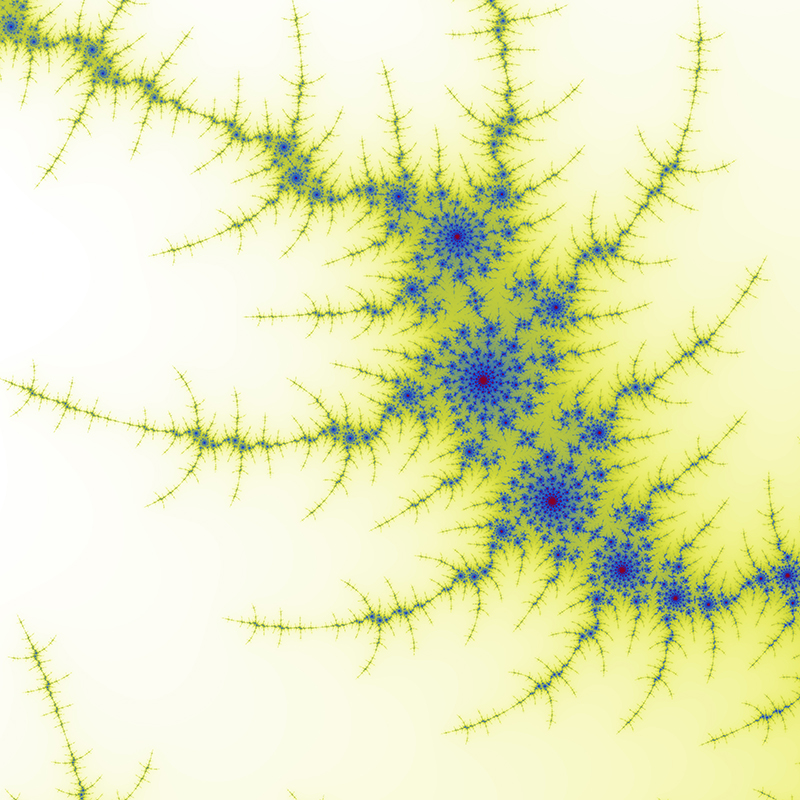
Zoom 3

The center of this sequence is (-1.62917,-0.0203968)

5

25

125

625

3125

15625

78125

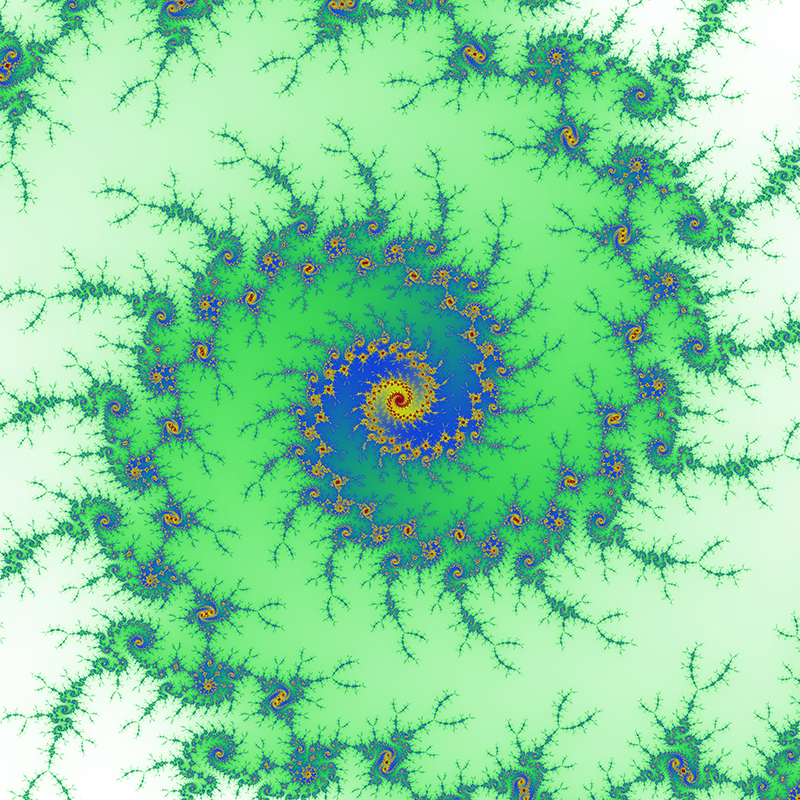
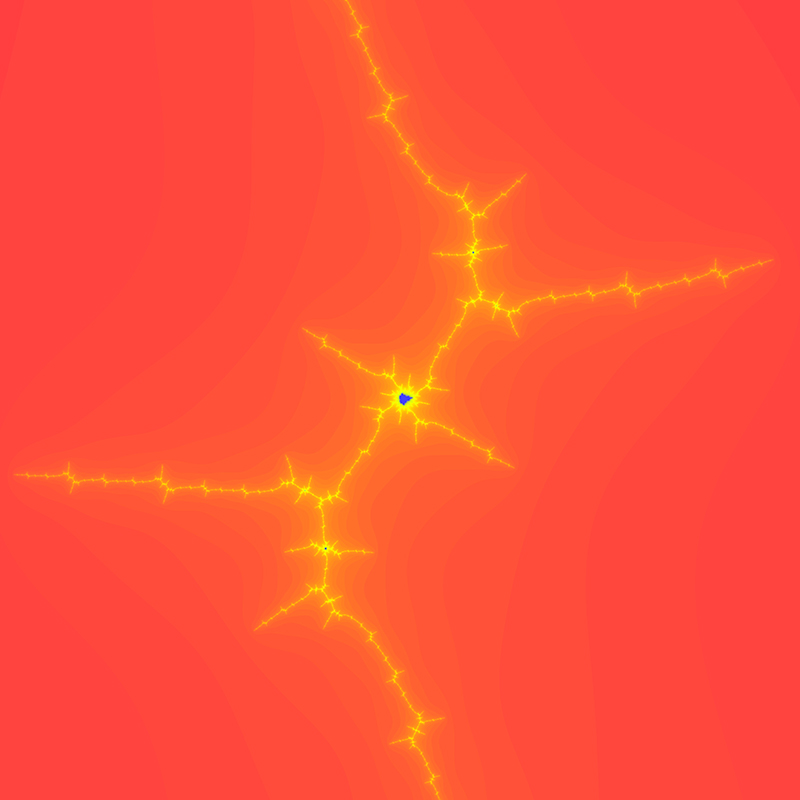
Zoom 4 - spirals

The center of this sequence is (-0.761574,-0.0847596)

5

25

125

625

3125

15625

78125

Source code

The following is a simple snippet of code that can be used to calculate the Mandelbrot by the somewhat inefficient brute force method.

/*
   Iterate a single point x0 + i y0 of the Mandelbrot for "imax" iterations.
   Return the number of iterations at which the point escapes.
   Return "imax" if the point doesn't escape.
*/
int Iterate(double x0,double y0,long imax)
{
   double x=0,y=0,xnew,ynew;
   int i;

   for (i=0;i<imax;i++) {
      xnew = x * x - y * y + x0;
      ynew = 2 * x * y + y0;
      if (xnew*xnew + ynew*ynew > 4)
         return(i);
      x = xnew;
      y = ynew;
   }

   return(imax);
}

Deep zoom images

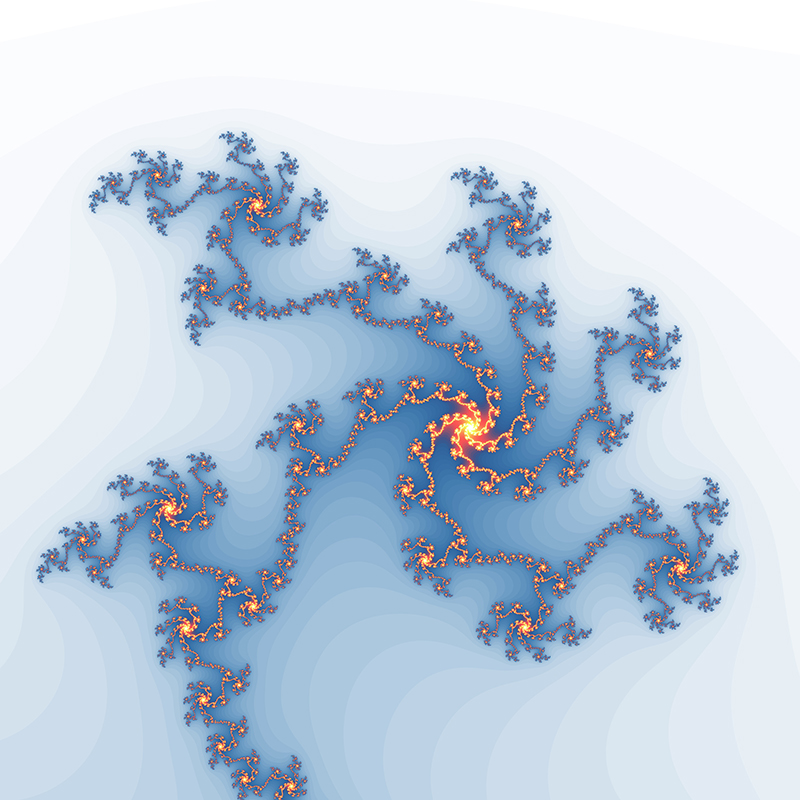
Examples

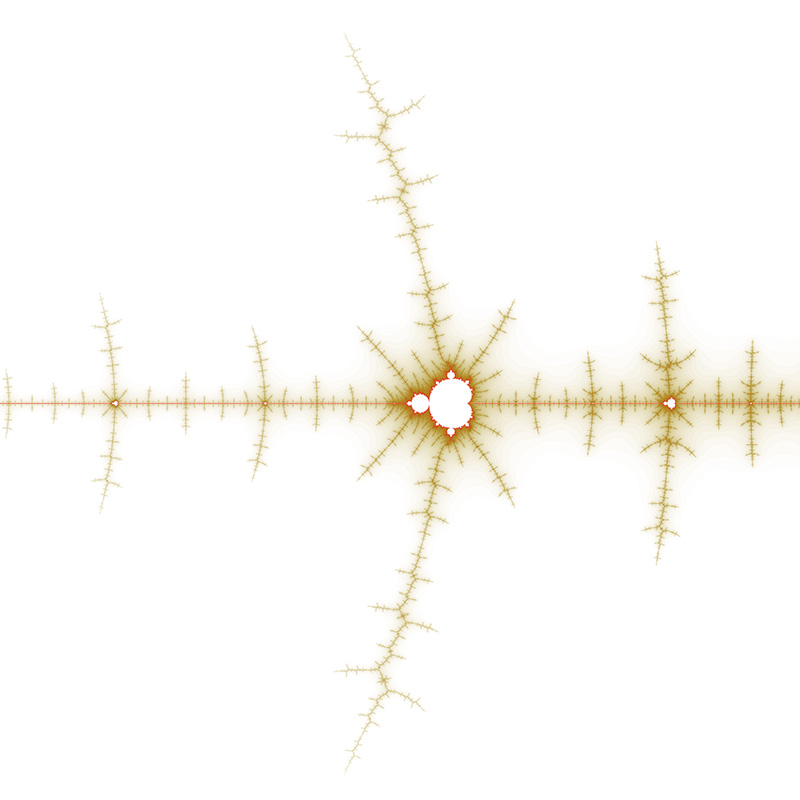
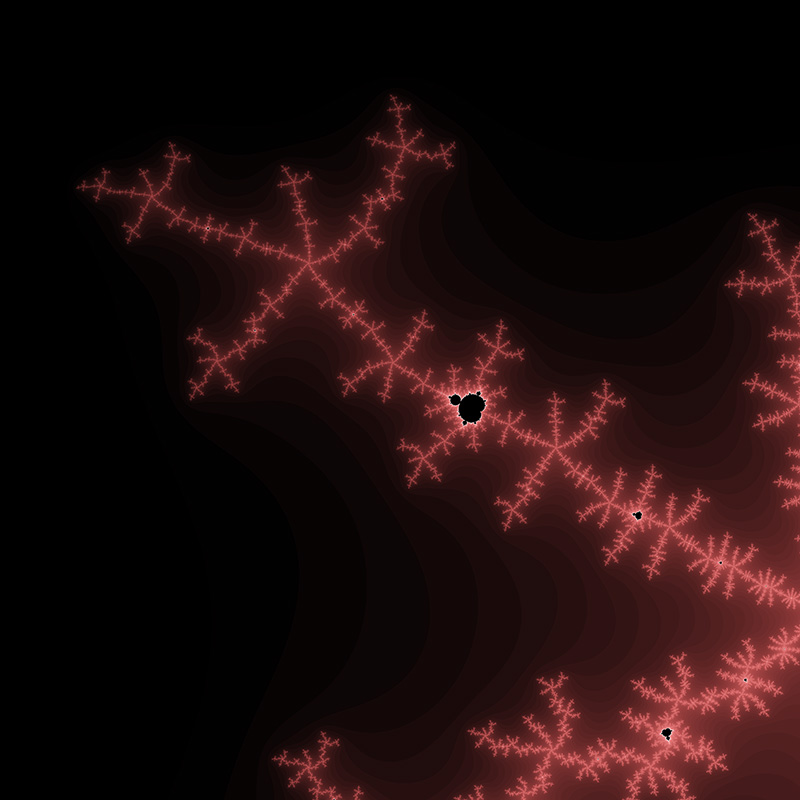
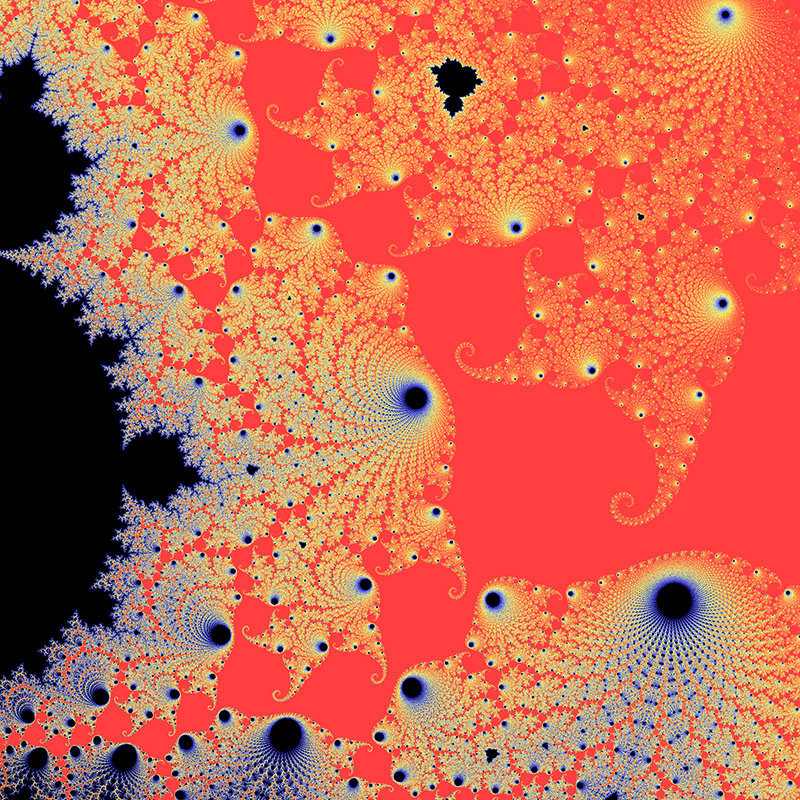
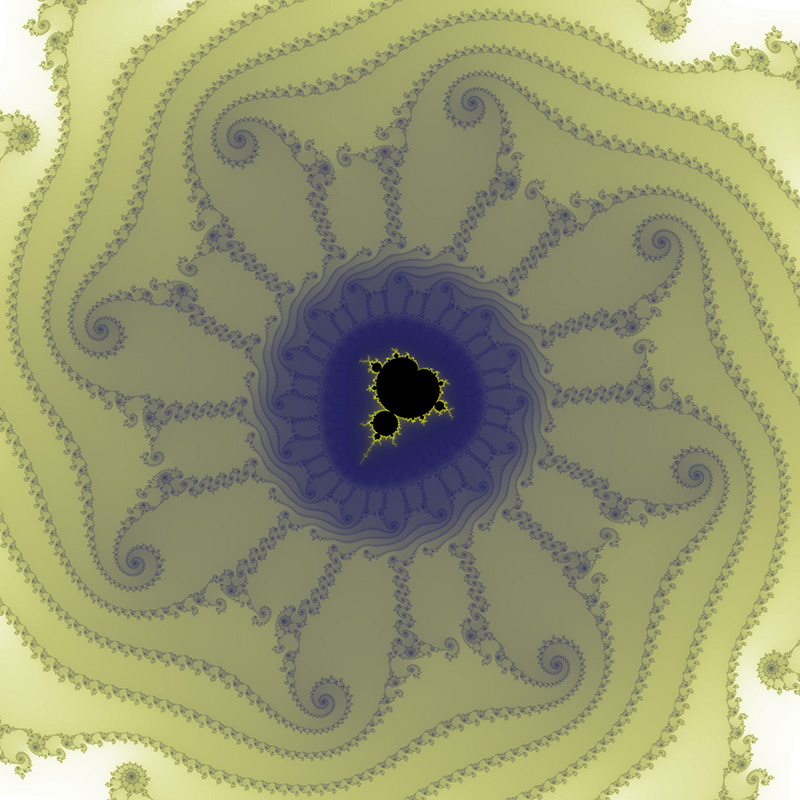Location courtesy of Tante Renate.
Position: -0.7746806106269039 -0.1374168856037867i Range: 1.506043553756164E-12

Inverse

The Mandelbrot doesn't exist outside a circle of radius 2 on the complex plane, this gives scope for turning it inside out by mapping z₀ to 1/z₀. The result, center at (1.4,0), is as follows.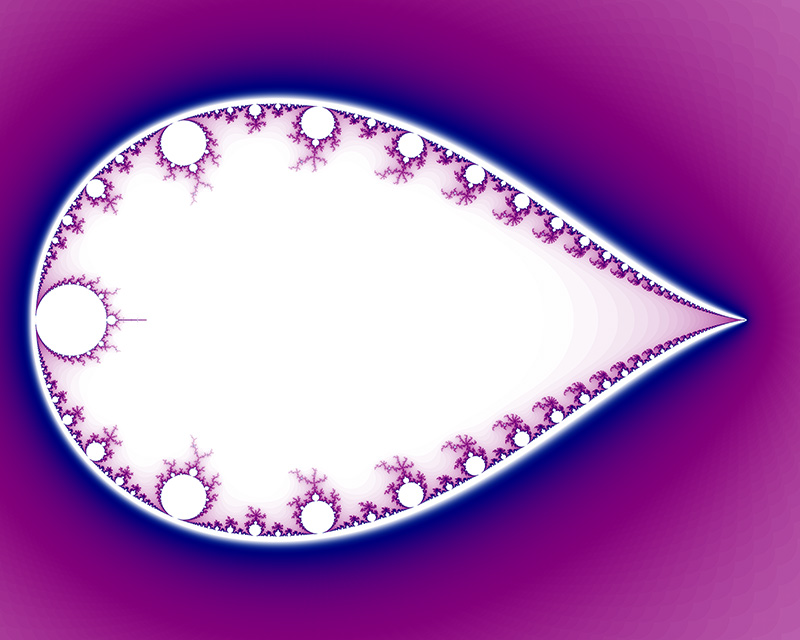

Wings

A relatively unexplored variation is to shade the plane based upon when the series decreases three times in succession. The Mandelbrot grow "wings" and discs at the peripheral points.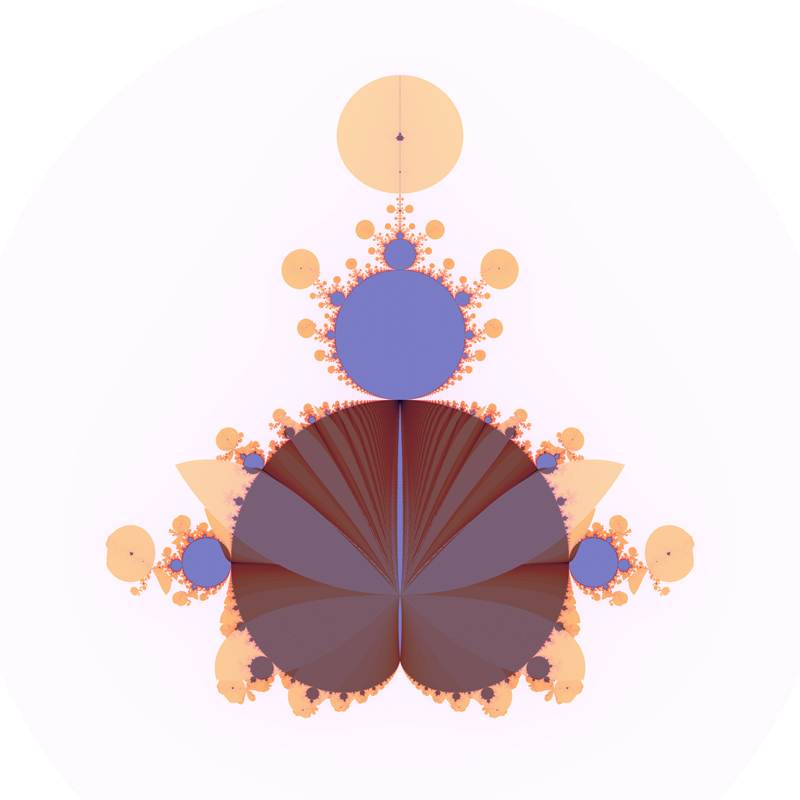

Contributions by Klaus Messner

x = -1.04180483110546, y = 0.346342664848392

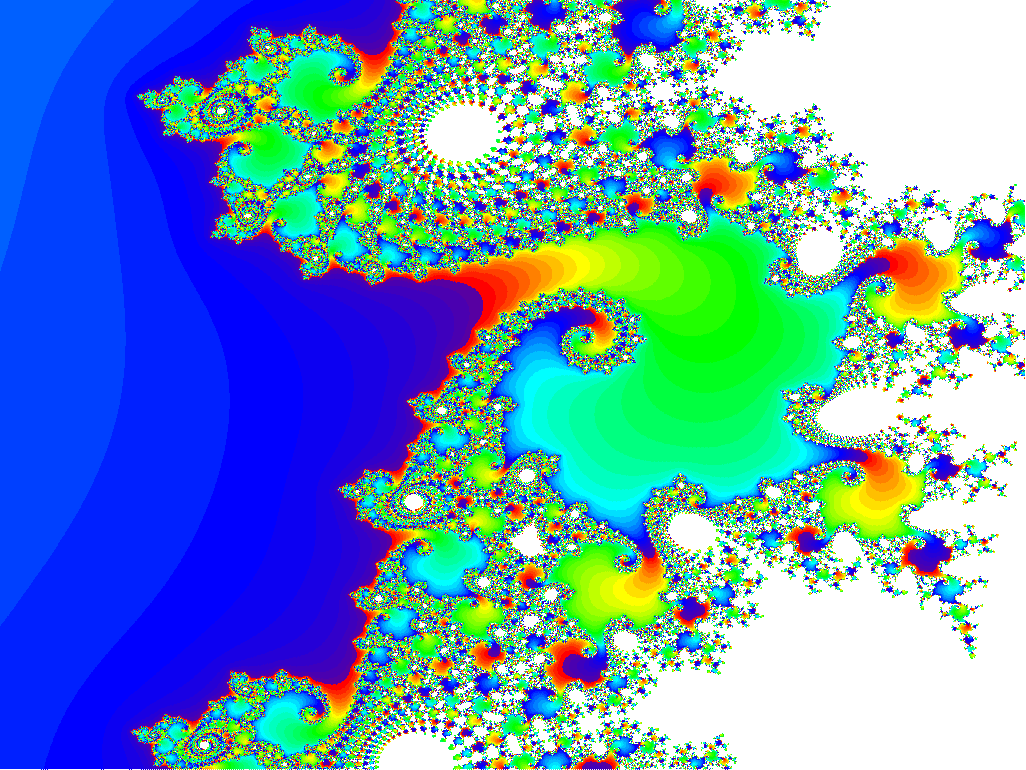x = -0.751095959125087, y = -0.116817186889238

x = -0.812223315621338, y = -0.185453926110785