Magnet 1Graphics by Paul BourkeJanuary 2018
The so call magnet fractal is created by looking at the convergence of the following series where "c" is each position on the complex plane making up the image. 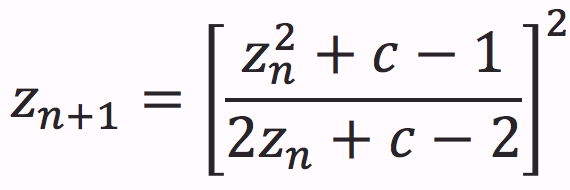
FracInt: These fractals use formulae derived from the study of hierarchical lattices, in the context of magnetic renormalisation transformations. This kinda stuff is useful in an area of theoretical physics that deals with magnetic phase-transitions (predicting at which temperatures a given substance will be magnetic, or non-magnetic). In an attempt to clarify the results obtained for real temperatures (the kind that you and I can feel), the study moved into the realm of Complex Numbers, aiming to spot Real phase-transitions by finding the intersections of lines representing Complex phase-transitions with the Real Axis. The first people to try this were two physicists called Yang and Lee, who found the situation a bit more complex than first expected, as the phase boundaries for Complex temperatures are (surprise!) fractals. 




Magnet 2Graphics by Paul BourkeJanuary 2018
The so call magnet fractal is created by looking at the convergence of the following series where "c" is each position on the complex plane making up the image. 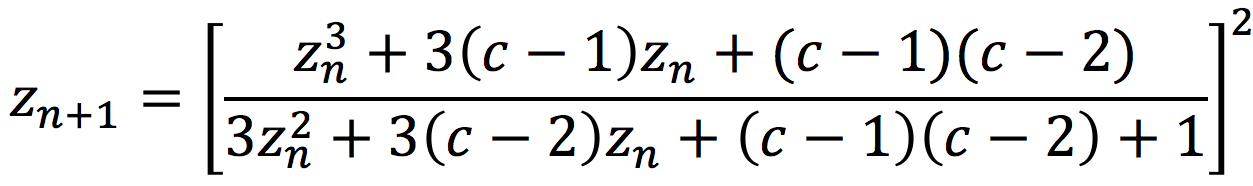
FracInt: These fractals use formulae derived from the study of hierarchical lattices, in the context of magnetic renormalisation transformations. This kinda stuff is useful in an area of theoretical physics that deals with magnetic phase-transitions (predicting at which temperatures a given substance will be magnetic, or non-magnetic). In an attempt to clarify the results obtained for real temperatures (the kind that you and I can feel), the study moved into the realm of Complex Numbers, aiming to spot Real phase-transitions by finding the intersections of lines representing Complex phase-transitions with the Real Axis. The first people to try this were two physicists called Yang and Lee, who found the situation a bit more complex than first expected, as the phase boundaries for Complex temperatures are (surprise!) fractals. 



|