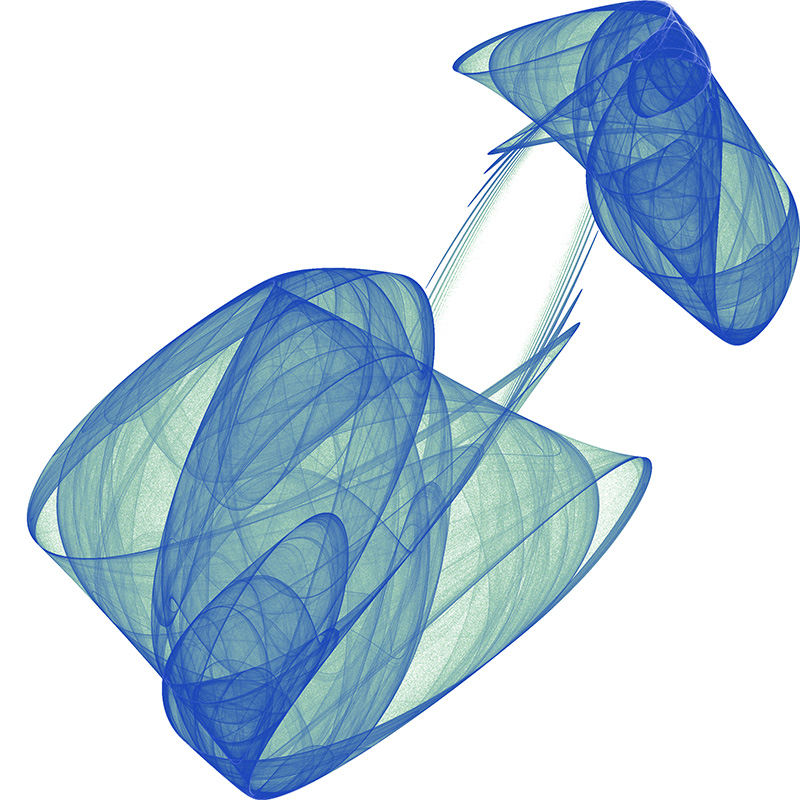
Random Attractors
Found using Lyapunov Exponents

In order for a system to exhibit chaotic behaviour it must be non linear. Representing chaotic systems on a screen or on paper leads one to considering a two dimensional system, an equation in two variables. One possible two dimensional non-linear system, the one used here, is the quadratic map defined as follows.

The standard measure for determining whether or not a system is chaotic is the Lyapunov exponent, normally represented by the lambda symbol. Consider two close points at step n, x_n and x_n+dx_n. At the next time step they will have diverged, namely to x_n+1 and x_n+1+dx_n+1. It is this average rate of divergence (or convergence) that the Lyapunov exponent captures. Another way to think about the Lyapunov exponent is as the rate at which information about the initial conditions is lost.

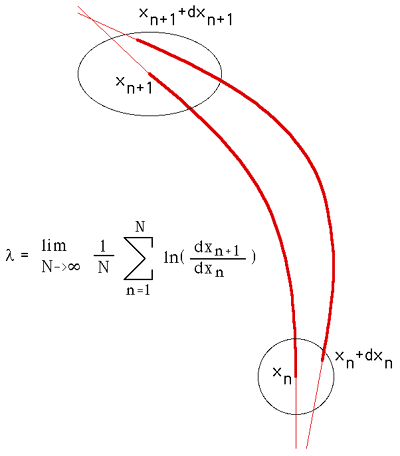
There are as many Lyapunov exponents as dimensions of the phase space. Considering a region (circle, sphere, hypersphere, etc) in phase space then at a later time all trajectories in this region form an n-dimensional elliptical region. The Lyapunov exponent can be calculated for each dimension. When talking about a single exponent one is normally referring to the largest, this convention will be assumed from now onwards.

If the Lyapunov exponent is positive then the system is chaotic and unstable. Nearby points will diverge irrespective of how close they are. Although there is no order the system is still deterministic! The magnitude of the Lyapunov exponent is a measure of the sensitivity to initial conditions, the primary characteristic of a chaotic system.

If the Lyapunov exponent is less than zero then the system attracts to a fixed point or stable periodic orbit. These systems are non conservative (dissipative). The absolute value of the exponent indicates the degree of stability.

If the Lyapunov exponent is zero then the system is neutrally stable, such systems are conservative and in a steady state mode.

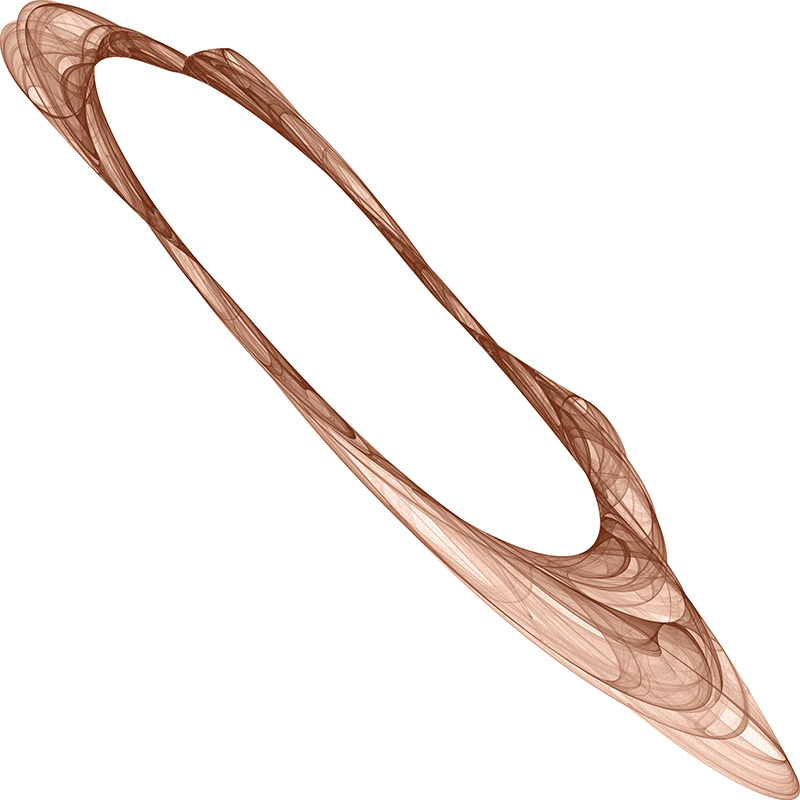
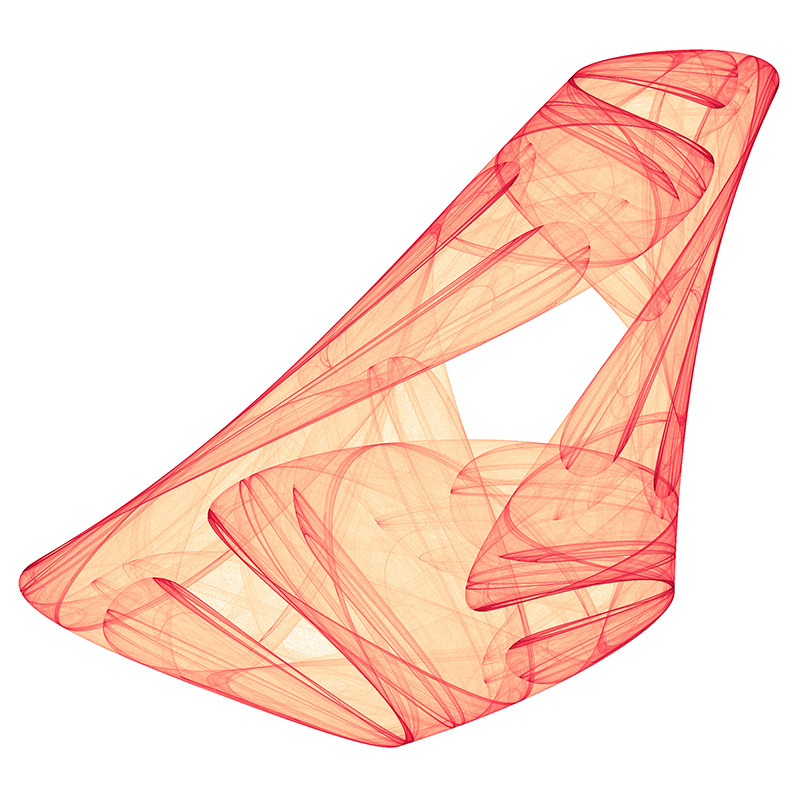
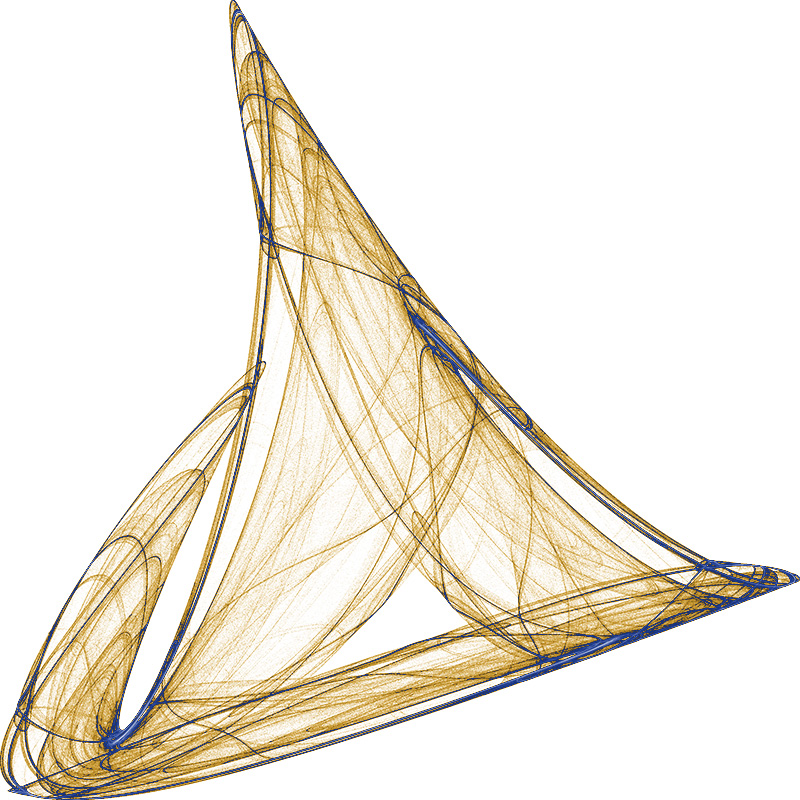
To create the chaotic attractors shown on this page each parameter a_n and b_n in the quadratic equation above is chosen at random between some bounds (+- 2 say). The system so specified is generated by iterating for some suitably large number of time steps (eg; 100000) steps during which time the image is created and the Lyapunov exponent computed. Note that the first few (1000) timesteps are ignored to allow the system to settle into its "natural" behaviour. If the Lyapunov exponent indicates chaos then the image is saved and the program moves on to the next random parameter set.

There are a number of ways the series may behave.

• It may converge to a single point, called a fixed point. These can be detected by comparing the distances between successive points. For numerical reasons this is safer than relying on the Lyapunov exponent which may be infinite (logarithm of 0)

• It may diverge to infinity, for the range (+- 2) used here for each parameter this is the most likely event. These are also easy to detect and discard, indeed they need to be in order to avoid numerical errors.

• It will form a periodic orbit, these are identified by their negative Lyapunov exponent.

• It will exhibit chaos, filling in some region of the plane. These are the solutions that "look good" and the ones we wish to identify with the Lyapunov exponent.

It should be noted that there may be visually appealing structures that are not chaotic attractors. That is, the resulting image is different for different initial conditions and there is no single basin of attraction. It's interesting how we "see" 3 dimensional structures in these essentially 2 dimensional systems.

The software used to create these images is given here: gen.c. On average 98% of the random selections of (a_n, b_n) result in an infinite series. This is so common because of the range (-2 <= a,b <= 2) for each of the parameters a and b, the number of infinite cases will reduce greatly with a smaller range. About 1% were point attractors, and about 0.5% were periodic basins of attraction.

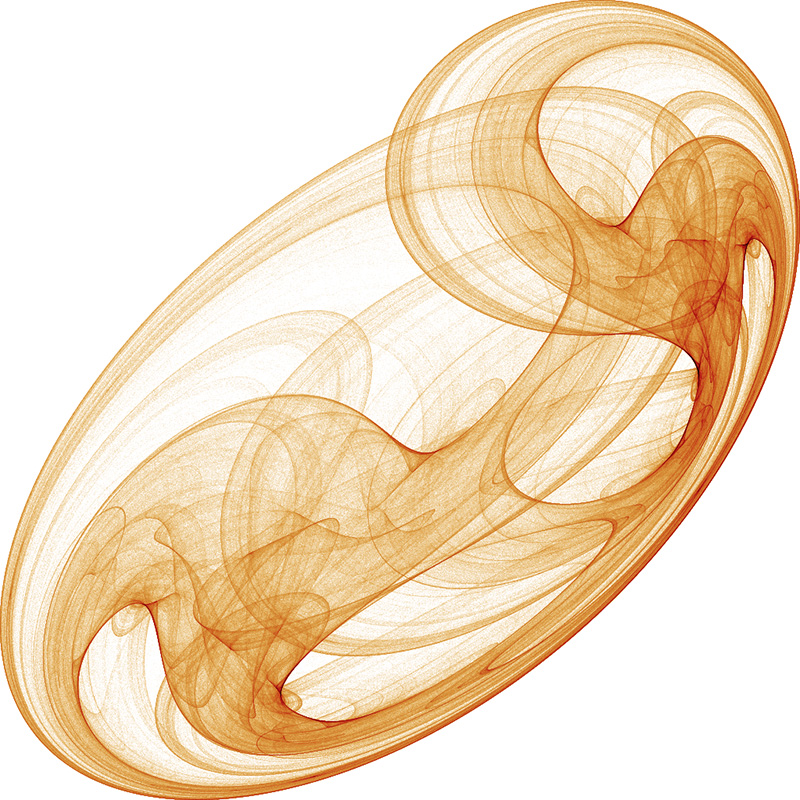
Image courtesy of Robert McGregor, Space Coast of Florida. Launch trail perhaps 30 minutes after the shuttle launch (June 2007) dispersing from a column into a smoke ring due to some unusual air currents in the upper atmosphere.

References

Berge, P., Pomeau, Y., Vidal, C.,
Order Within Chaos, Wiley, New York, 1984.

Crutchfield, J., Farmer, J., Packard, N.
Chaos, Scientific American, 1986, 255, 46-47

Das, A., Das, Pritha, Roy, A
Applicability of Lyapunov Exponent in EEG data analysis. Complexity International, draft manuscript.

Devaney, R.
An Introduction to Chaotic Dynamical Systems, Addison-Wesley, 1989

Feigenbaum, M.,
Universal behaviour in Nonlinear Systems, Los Alamos Science, 1981

Peitgen, H., Jurgens, H., Saupe, D
Lyapunov exponents and chaotic attractors in Chaos and fractals - new frontiers of science. Springer, new York, 1992.

Contributions by Dmytry Lavrov