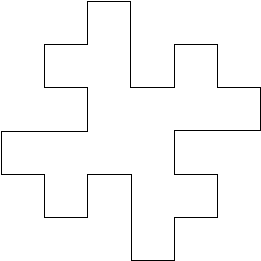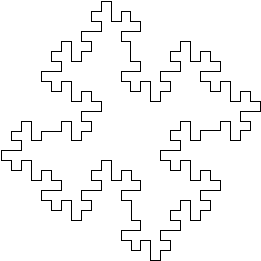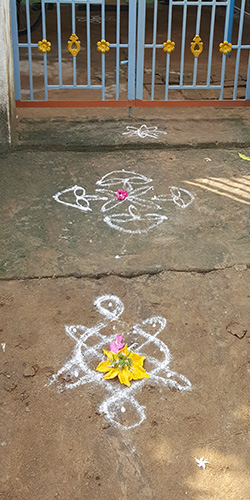L-System User Notes(Lindenmayer Systems)Written by Paul Bourke Version 2.5, July 1991
Introduction This program implements some of the L-Systems discussed in "Lecture Notes in Biomathematics" by Przemyslaw Prusinkiewcz and James Hanan. A brief description of an 0L system will be presented here but for a more complete description the user should consult the literature. The application was initially written to investigate methods of incorporating objects with a large number of drawing elements (lines, polygons) into a CAD package. L Systems is one way for example of "generating" trees at the rendering stage but not during the editing stage where the image complexity will slow down the response time. Simple example of a 0L system
A string of characters (symbols) is rewritten on each iteration according to some replacement rules. Consider an initial string (axiom) and a rewriting rule
After one iteration the following string would result
For the next iteration the same rule is applied but now to the string resulting from the last iteration F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F
Some symbols are now given a graphical meaning, for example, F means move forward drawing a line, + means turn right by some predefined angle (90 degrees in this case), - means turn left. Using these symbols the initial string F+F+F+F is just a rectangle (ø = 90). The replacement rule F --> F+F-F-FF+F+F-F replaces each forward movement by the following figure 
Character Meaning
F Move forward by line length drawing a line
f Move forward by line length without drawing a line
+ Turn left by turning angle
- Turn right by turning angle
| Reverse direction (ie: turn by 180 degrees)
[ Push current drawing state onto stack
] Pop current drawing state from the stack
# Increment the line width by line width increment
! Decrement the line width by line width increment
@ Draw a dot with line width radius
{ Open a polygon
} Close a polygon and fill it with fill colour
> Multiply the line length by the line length scale factor
< Divide the line length by the line length scale factor
& Swap the meaning of + and -
( Decrement turning angle by turning angle increment
) Increment turning angle by turning angle increment
When drawing the graphical representation of the L string all other characters are ignored. The user may choose and use any other single printable characters for the replacement rules except, note: this excludes "white" characters such as spaces and tabs. For context sensitive L systems the * character is used to represent any match. See the SYMBOL menu item for a summary of the reserved symbols. Menus
Advanced features/comments
Heinz-Otto and Deitmar Saupe. The Science of Fractal Images. Springer-Verlag Przemyslaw Prusinkiewicz. Application of L-Systems to Computer Imagery. Lecture Notes in Computer Science #291, Pages 534-548 Przemyslaw Prusinkiewicz, James Hanan. Lecture Notes in Biomathematics #79 Prusinkiewicz, P. Graphical Applications of L-Systems. Proc. of Graphics Interface 1986 - Vision Interface, 1986, Pages 247-253. Smith, A.R. Plants, Fractals, and Formal Languages. Computer Graphics, 18, 3, 1984, Pages 1-10 Prusinkiewicz, P and Lindenmayer A. The Algorithmic Beauty of Plants. Springer Verleg, 1990, Pages 40-50
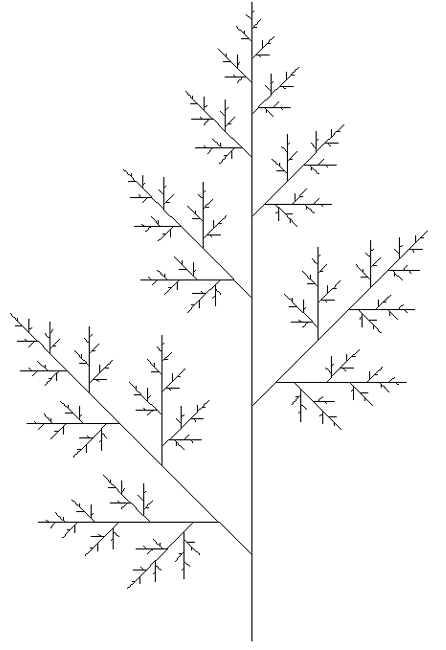
L-System LeafWritten by Paul Bourke
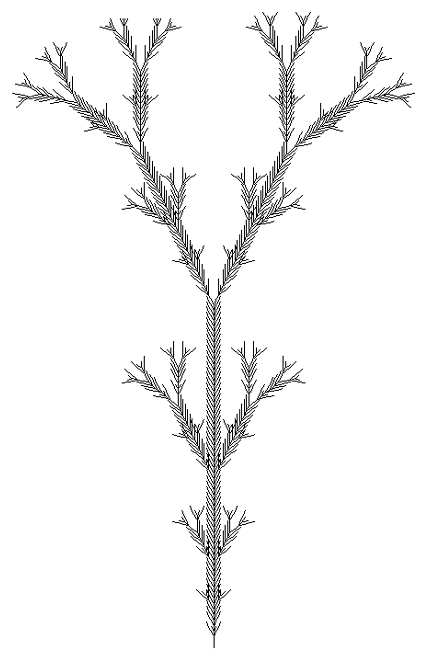
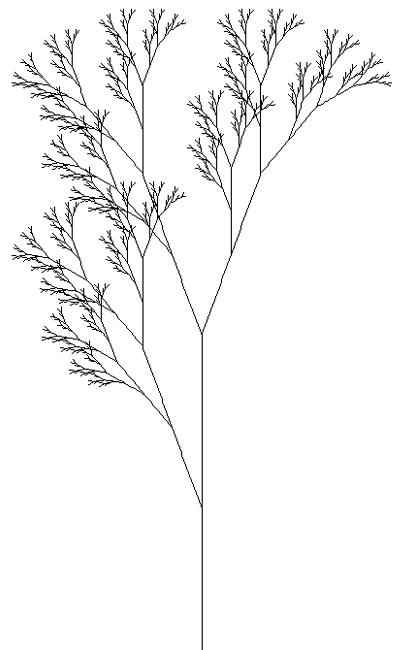
L-System BushesWritten by Paul Bourke
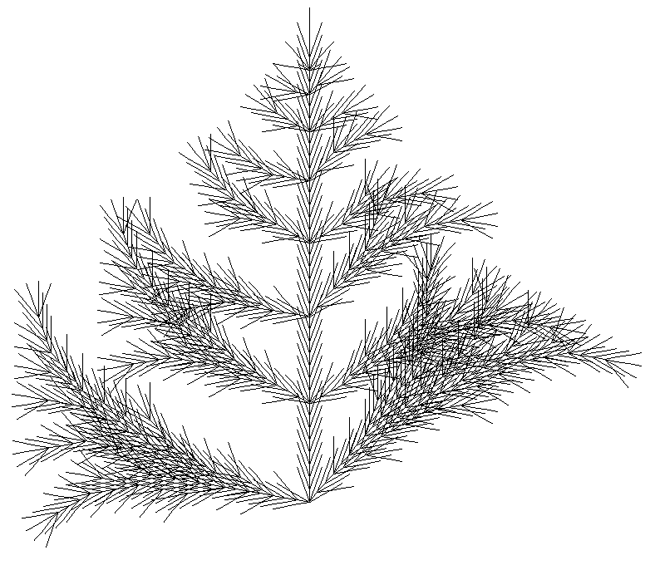
Attributed to Saupe
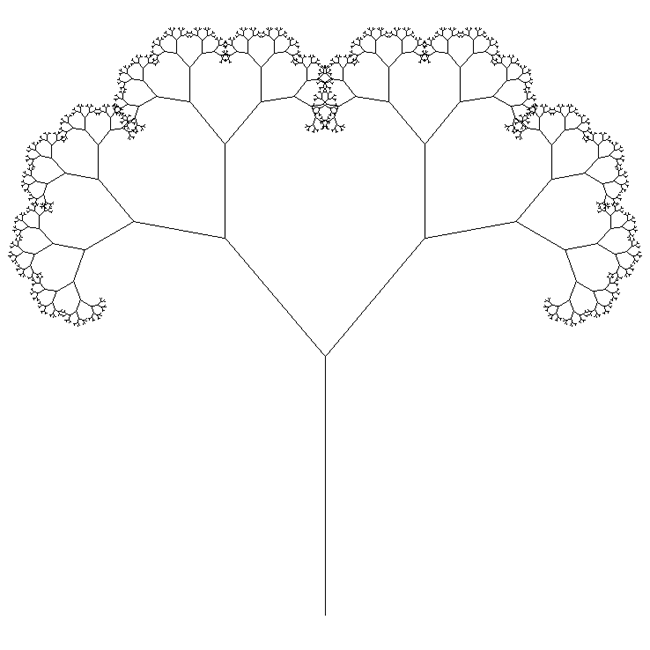
  L-System sticksWritten by Paul Bourke
L-System algaeWritten by Paul Bourke
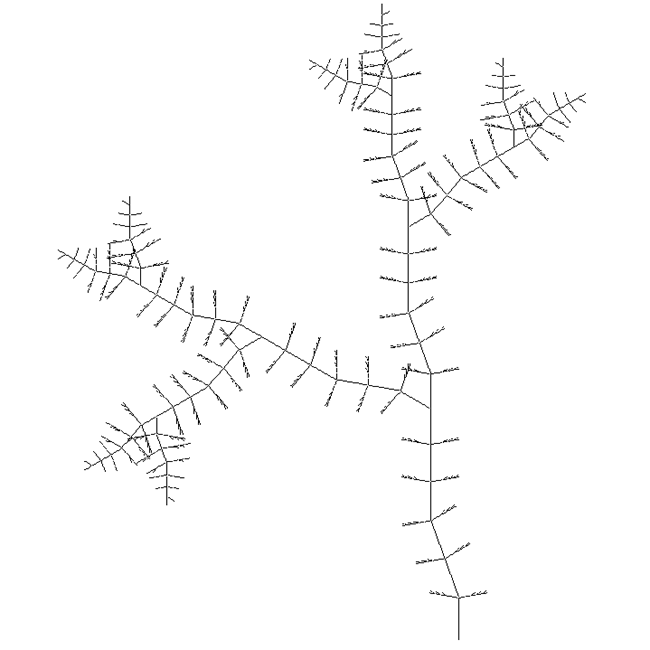
L-System WeedWritten by Paul Bourke
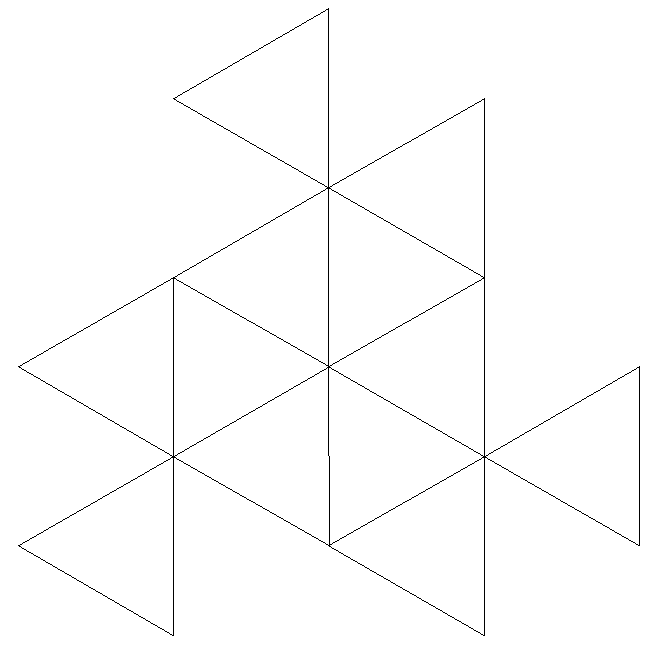
TriangleWritten by Paul BourkeJuly 1990 L-Systems
axiom = F+F+F
 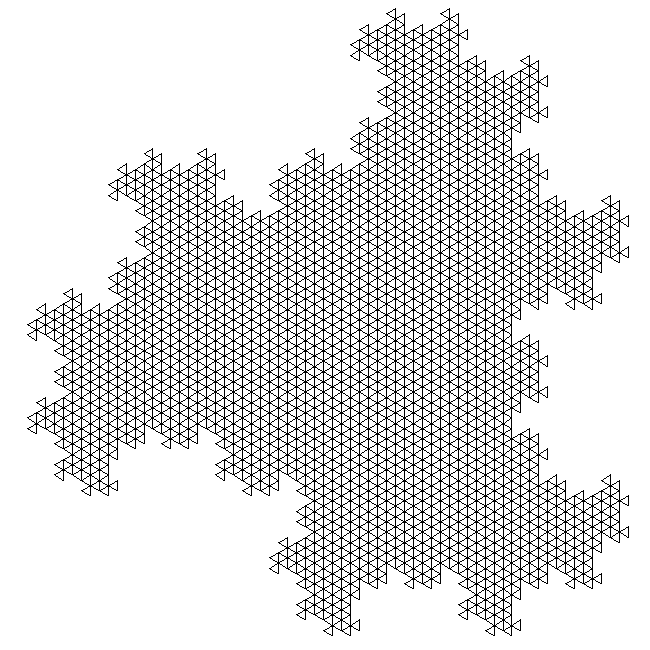
As an IFS
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3
a 0.0 0.0 0.0
b 0.577 0.577 0.577
c -0.577 -0.577 -0.577
d 0.0 0.0 0.0
e 0.0951 0.4413 0.0952
f 0.5983 0.7893 0.9893
probability 1/3 1/3 1/3
Quadratic GosperWritten by Paul BourkeJune 1990 Attributed to Dekking, 1982
axiom = -YF



Square SierpinskiWritten by Paul BourkeAugust 1990 First reported circa 1912
axiom = F+XF+F+XF





CrystalWritten by Paul BourkeJune 1990
axiom = F+F+F+F






Derby, Western Australia
Peano CurveWritten by Paul BourkeJune 1990 First documented circa 1890
axiom = X
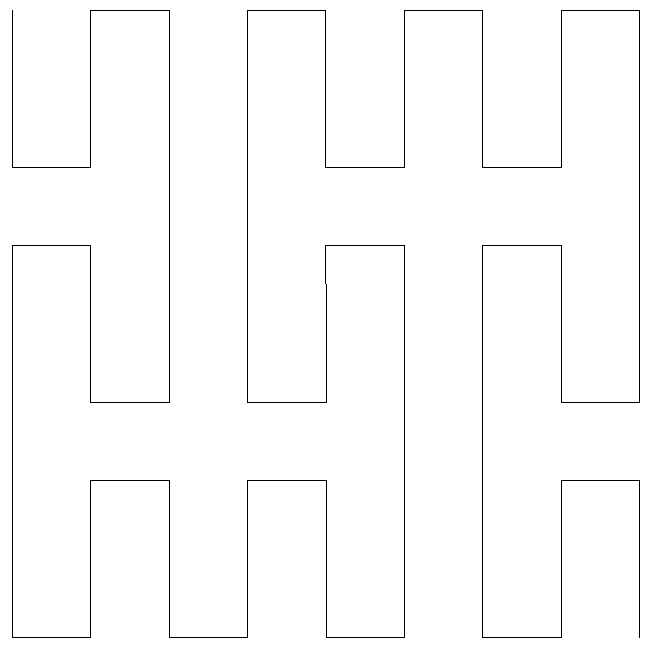 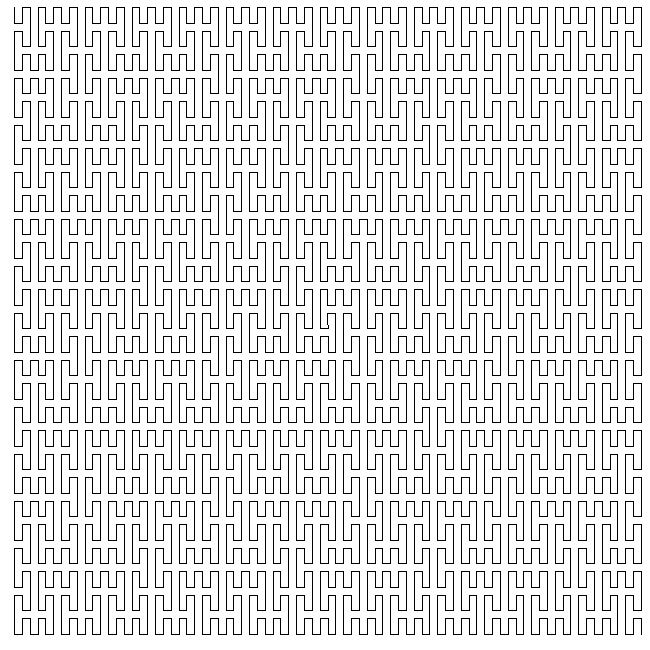
Quadratic SnowflakeWritten by Paul BourkeJuly 1990
axiom = F
Variation by Hasan Hosam.

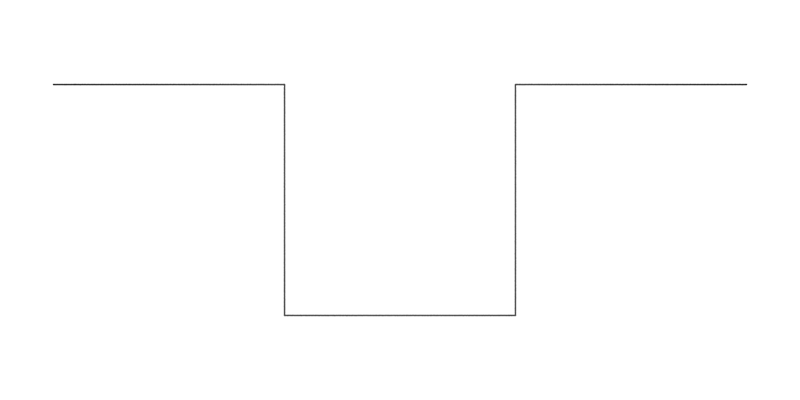
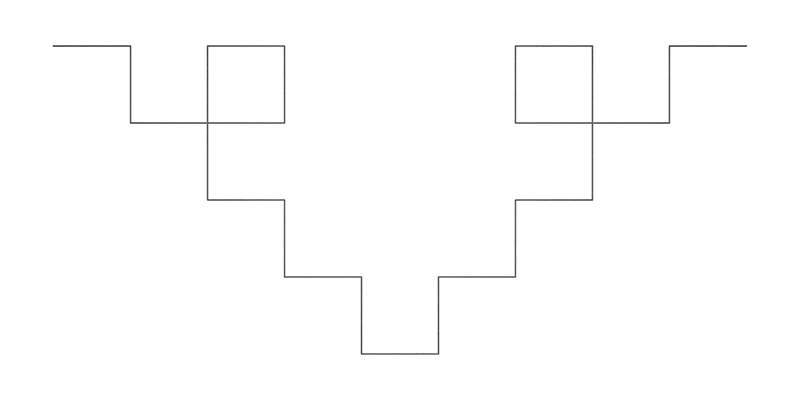
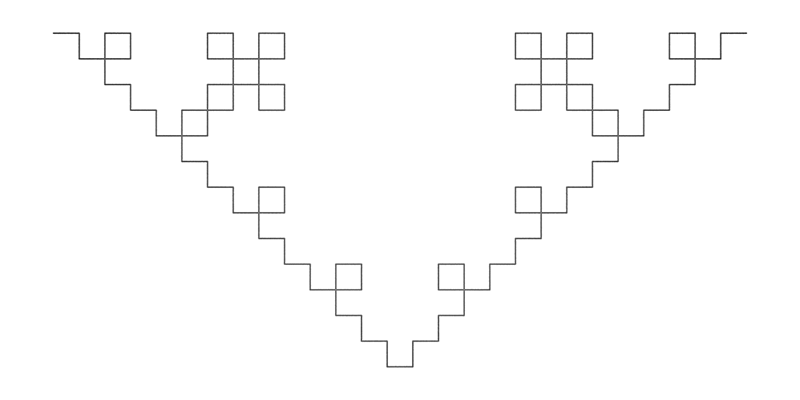
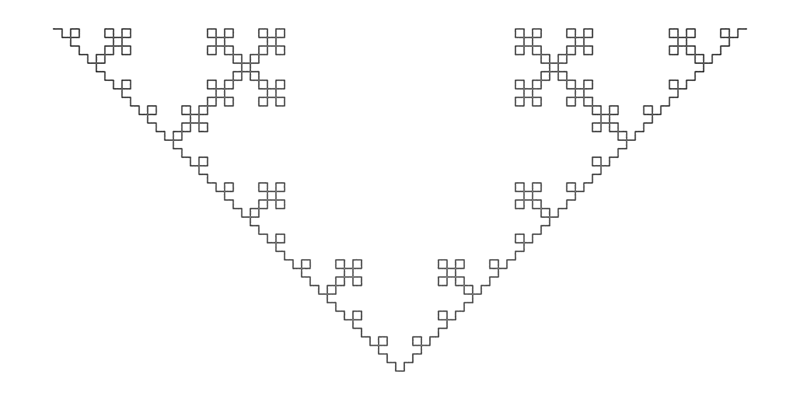
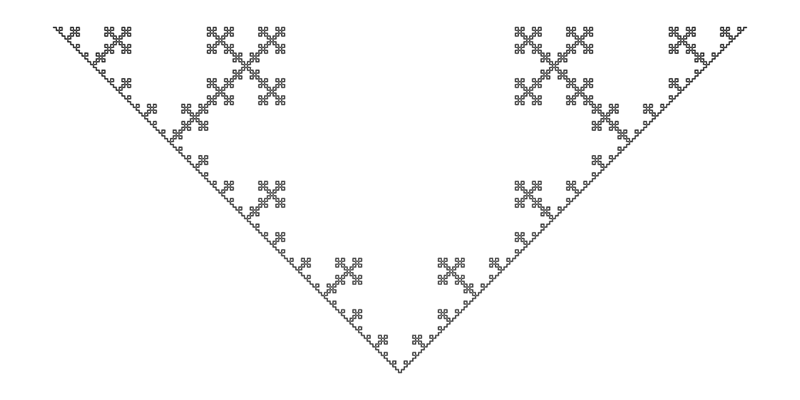
Quadratic Koch IslandWritten by Paul BourkeJuly 1990
axiom = F+F+F+F
 String length: 567
 String length: 5103
 String length: 45927




Variation by Hasan Hosam.

Koch CurveWritten by Paul BourkeJune 1990 Fractal Dimension: 1.5
axiom = F+F+F+F




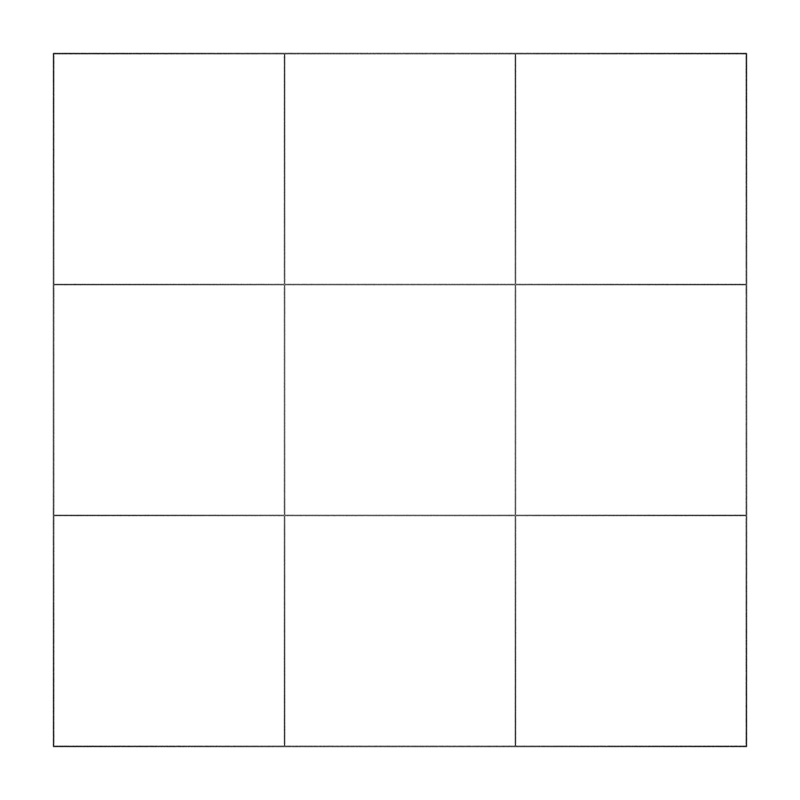
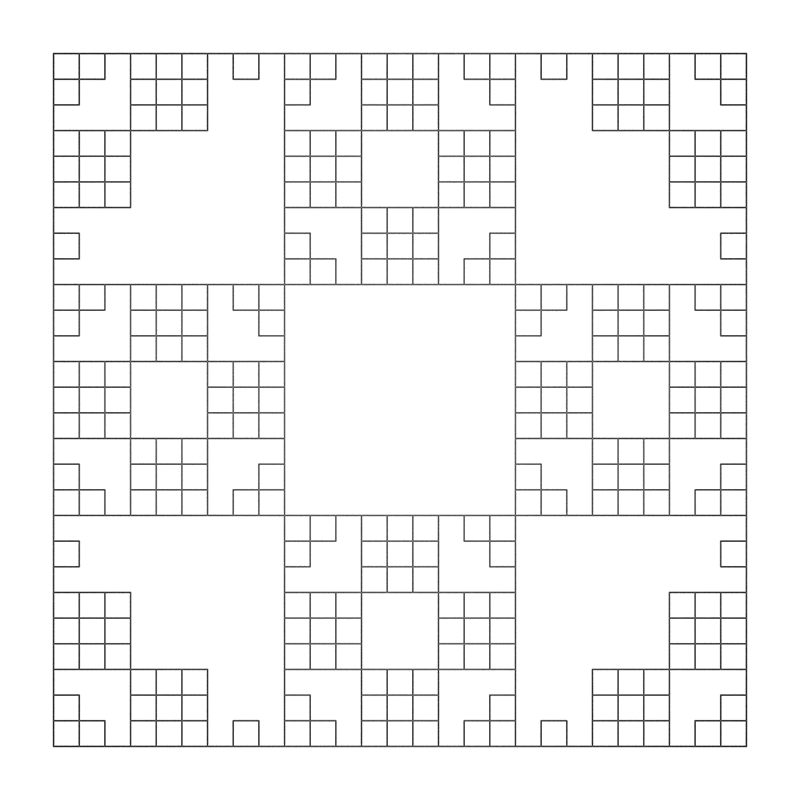
BoardWritten by Paul BourkeJune 1990
axiom = F+F+F+F


HilbertWritten by Paul BourkeJune 1990 Attributed to the German mathematician David Hilbert, circa 1891
axiom = X





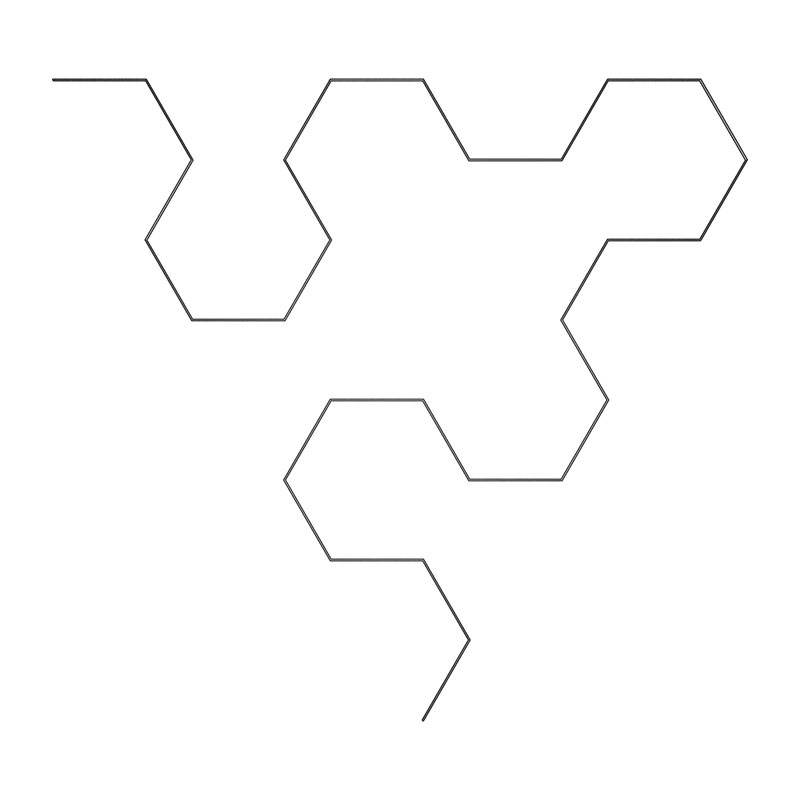
Sierpinski ArrowheadWritten by Paul BourkeJune 1990
axiom = YF YF+XF+YF-XF-YF-XF-YF+XF+YF 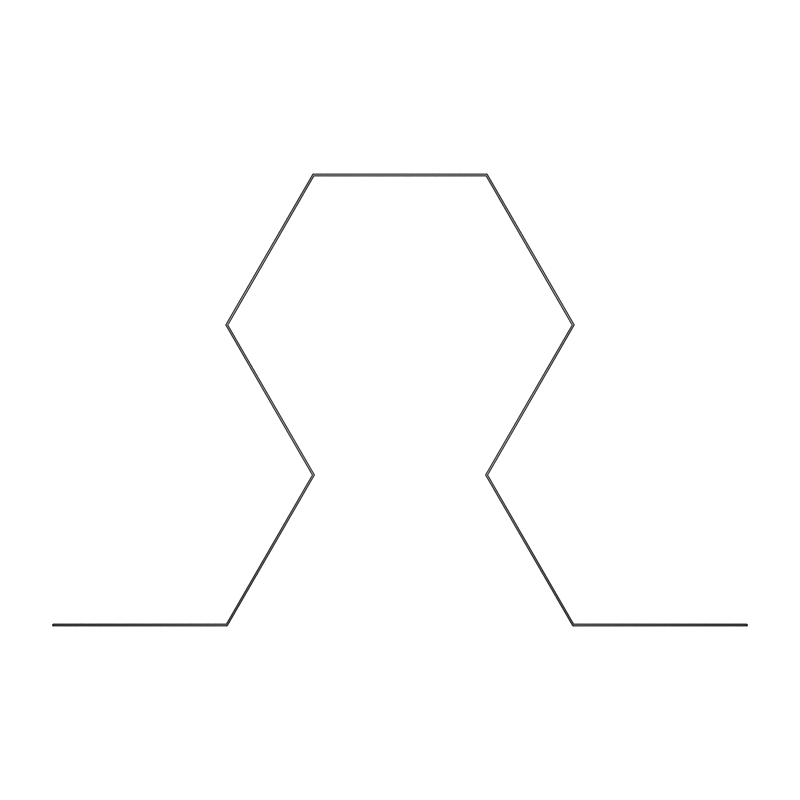
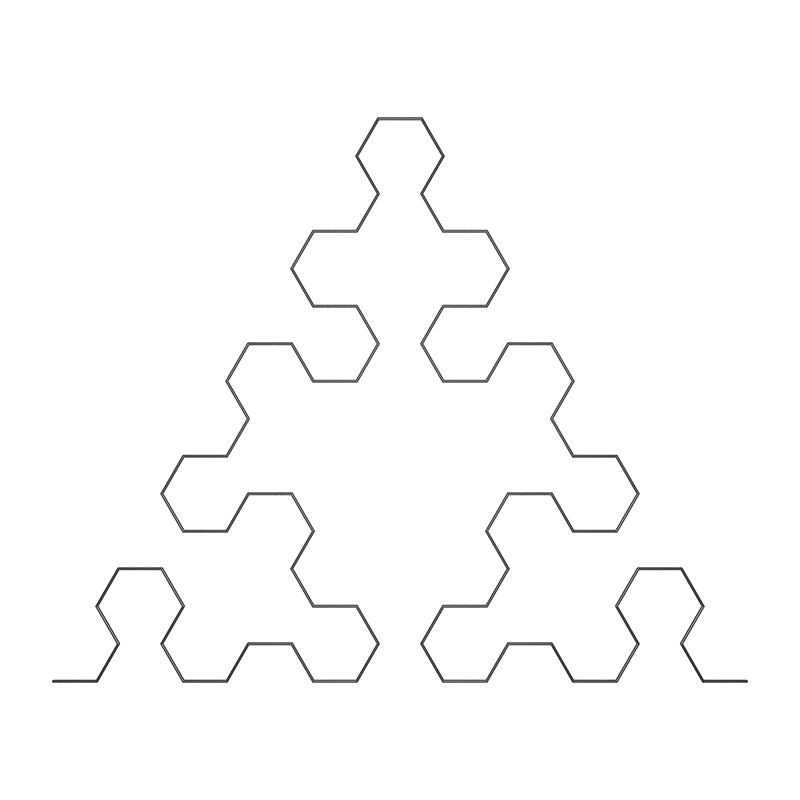

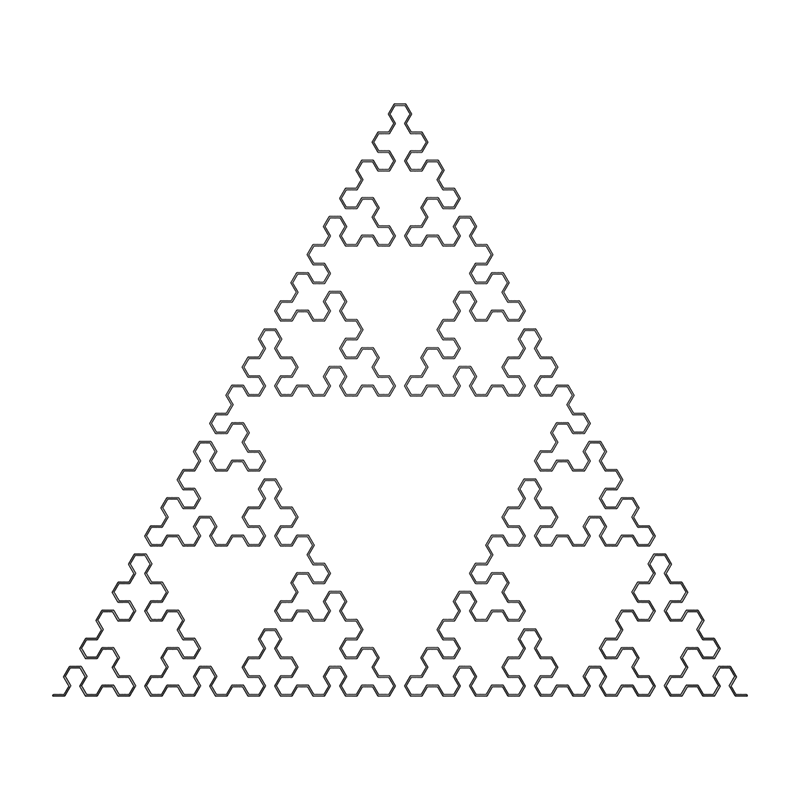

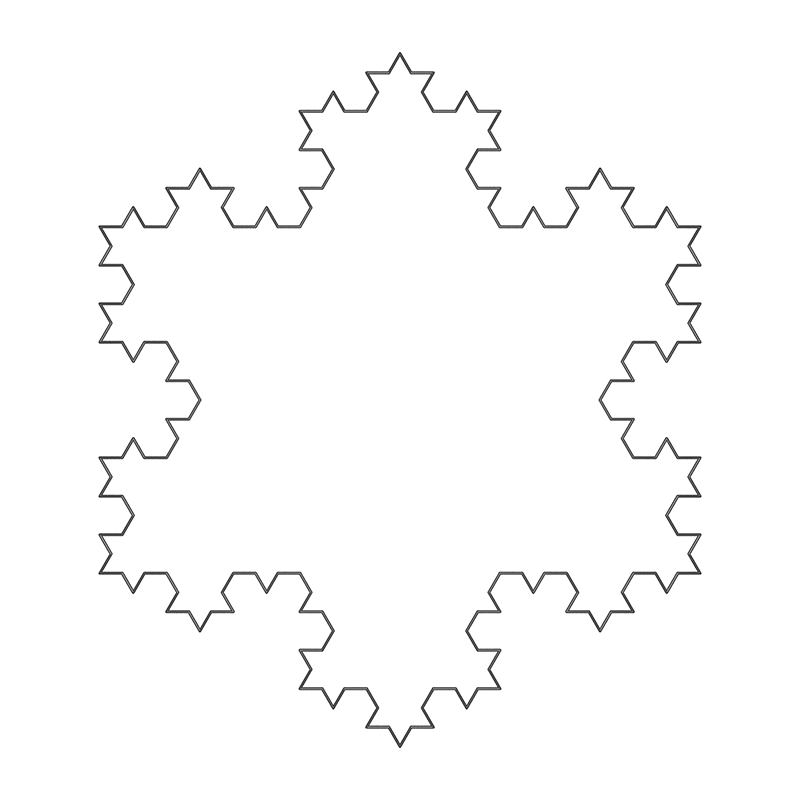
Von Koch SnowflakeWritten by Paul BourkeJune 1990 Fractal Dimension: log(4)/log(3) = 1.262 L-Systems
axiom = F++F++F


 IFS
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3 set 4
a 0.3330 0.3330 0.1670 0.1670
b 0.0000 0.0000 -0.2890 0.2890
c 0.0000 0.0000 0.2890 -0.2890
d 0.3330 0.3330 0.1670 0.1670
e -0.3330 0.3330 -0.0830 0.0830
f 0.0000 0.0000 0.1440 0.1440
CrossWritten by Paul BourkeJune 1990
axiom = F+F+F+F





CrossWritten by Paul BourkeAugust 1990
axiom = F+F+F+F





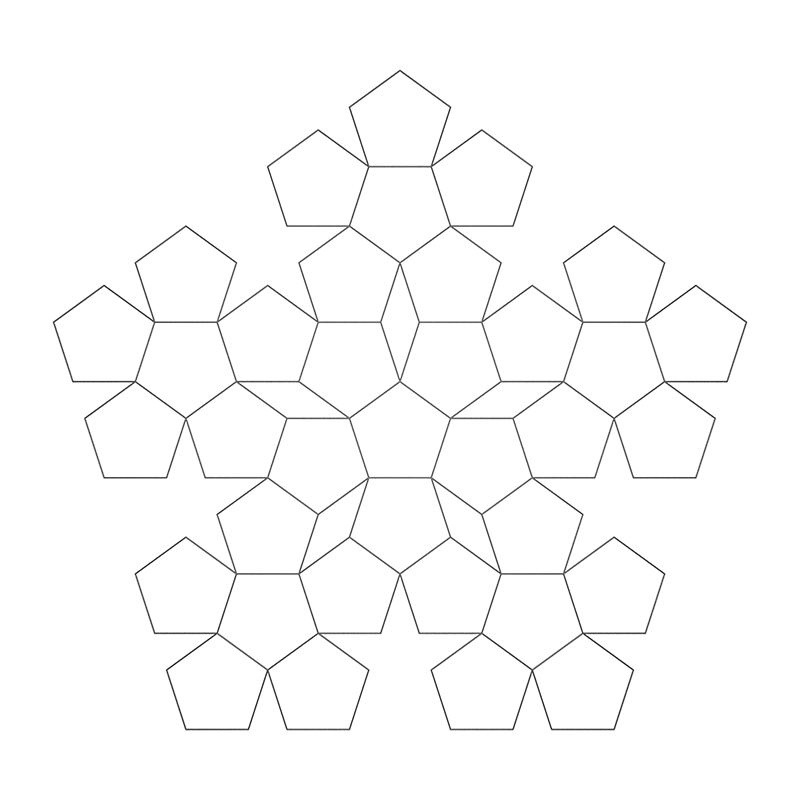
PentaplexityWritten by Paul BourkeSeptember 1990
axiom = F++F++F++F++F
If your L-Systems software doesn't support the "|" symbol (like the implementation in the PGF/TikZ), then just replace the "|" with "+++++". 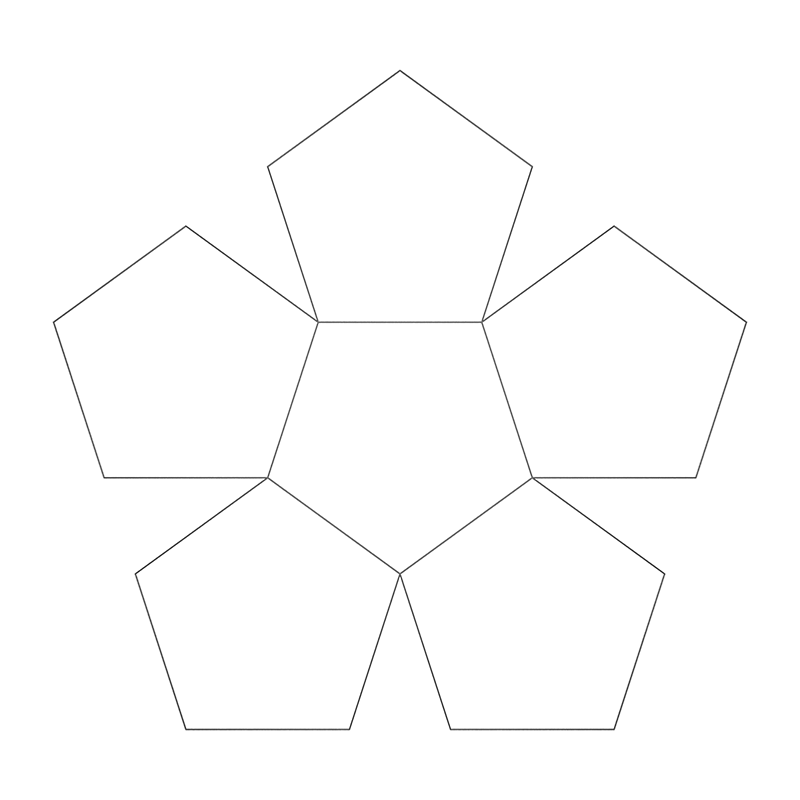


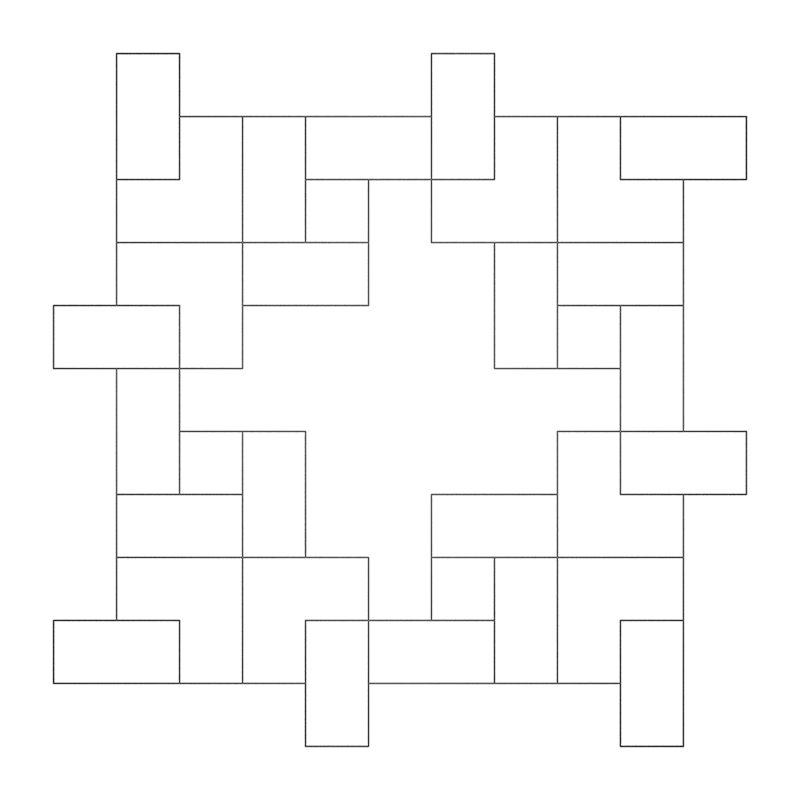
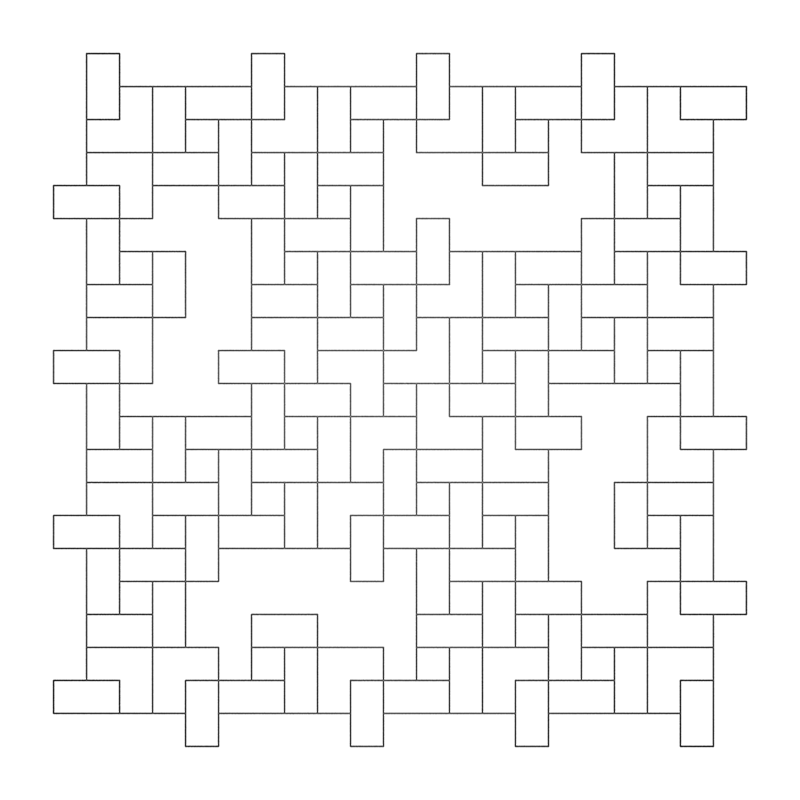
TilesWritten by Paul BourkeJune 1990 Fractal Dimension: log(7)/log(3) = 1.771
axiom = F+F+F+F



RingsWritten by Paul BourkeJune 1990
axiom = F+F+F+F




Dragon CurveWritten by Paul BourkeAugust 1990 Attributed to David and Knuth, 1970
axiom = FX






Hexagonal GosperWritten by Paul BourkeJuly 1990 Attributed to Mandelbrot, 1982
axiom = XF





Lévy curveWritten by Paul BourkeFebruary 2019
axiom = F
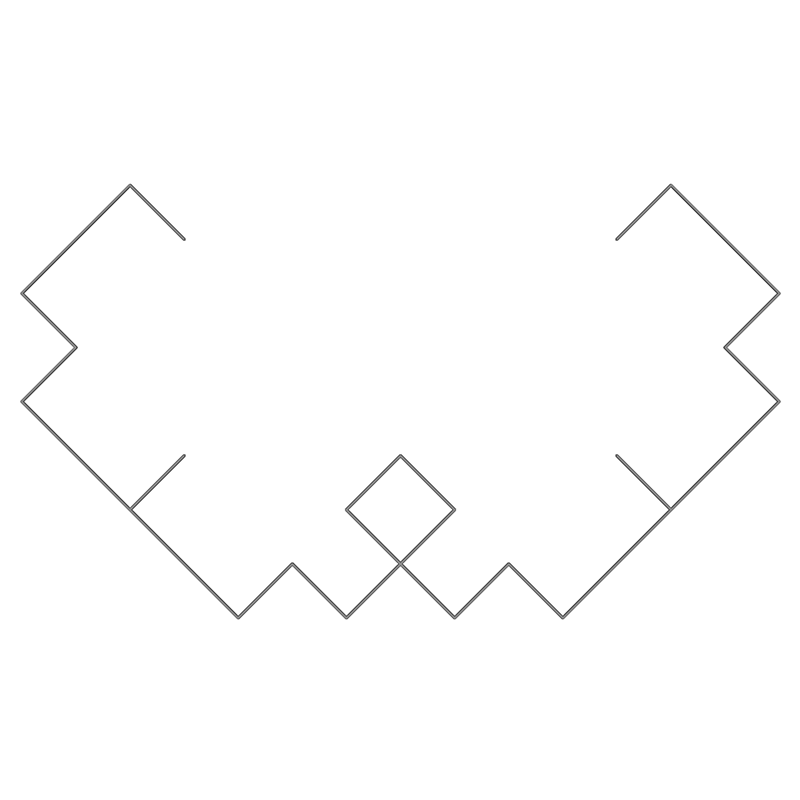
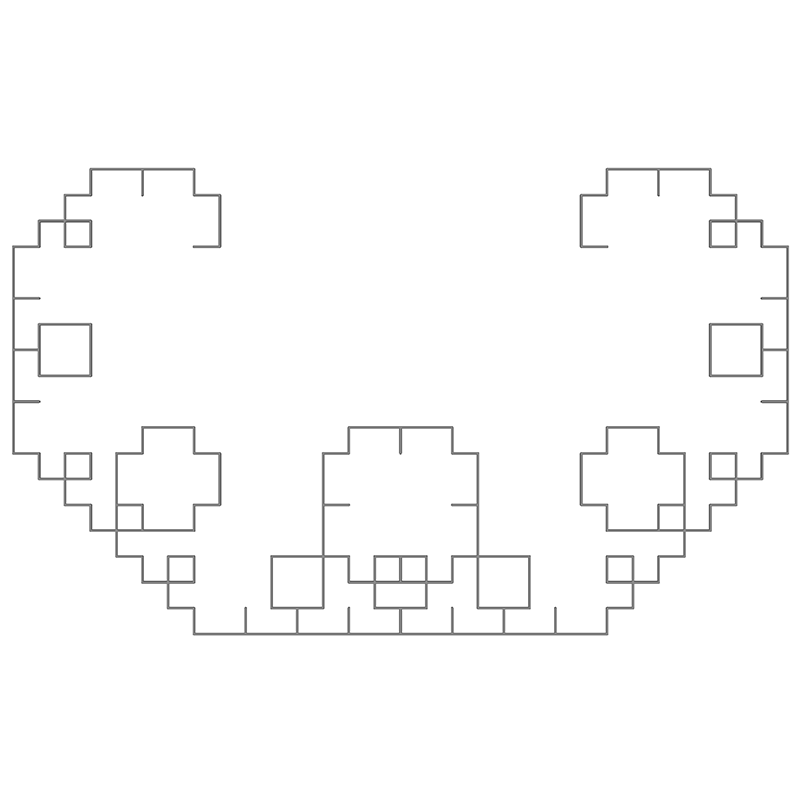

Classic Sierpinski CurveWritten by Paul BourkeRules by Chris Wallace November 2019
axiom = F--XF--F--XF
Krishna AnkletsWritten by Paul Bourke
axiom = -X--X
Mango LeafWritten by Paul Bourke
axiom = Y---Y
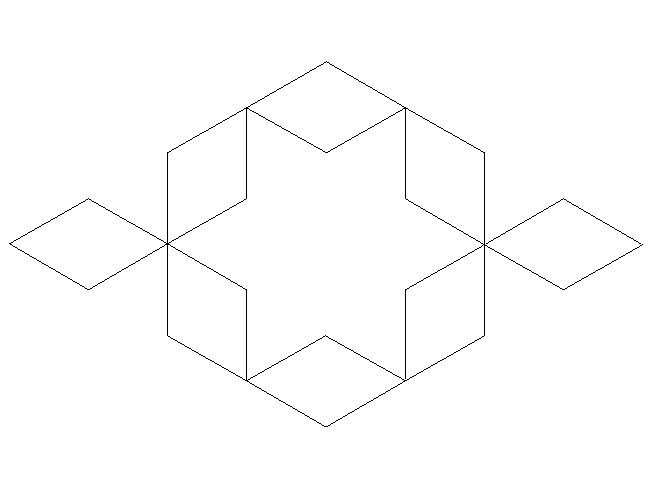 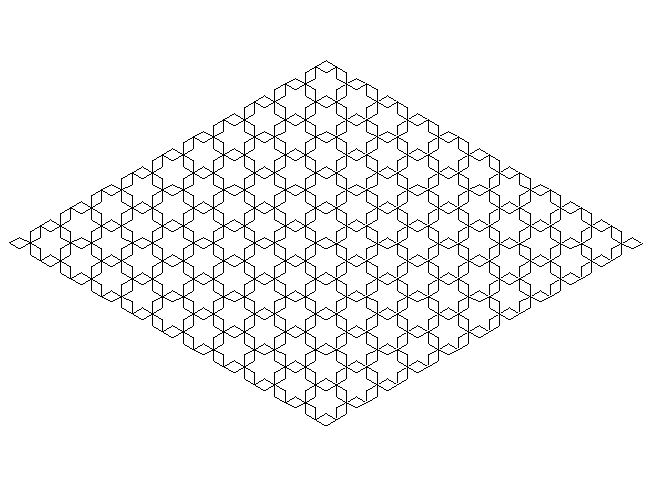
Snake KolamWritten by Paul Bourke
axiom = F+XF+F+XF
 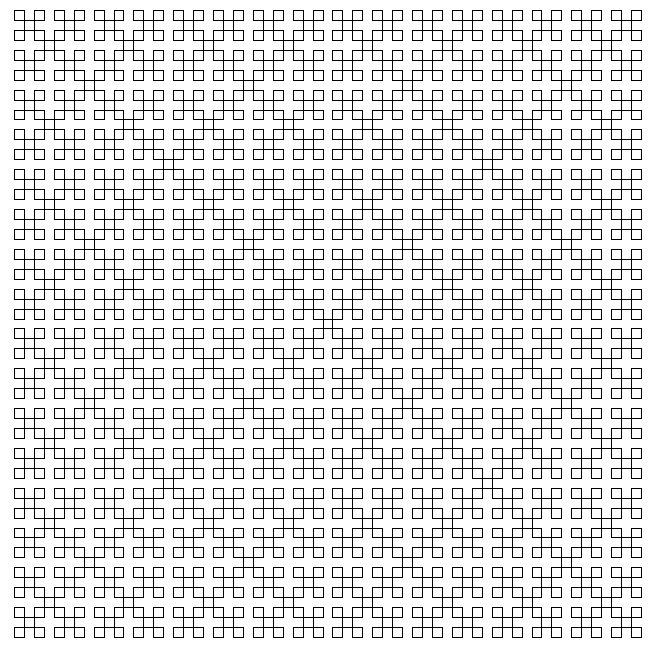
KolamJanuary 2019
axiom = (-D--D)
 Kolam patterns from the South of India, drawn by rice powder in front of houses every morning before the doorway is used.
|