The Lorenz Attractor in 3DImages by Paul BourkeApril 1997 MSWindows application by Dominic van Berkel.
Listen (mov or midi) to the
Lorenz attractor. lorenz.m4v for an iPod-video.
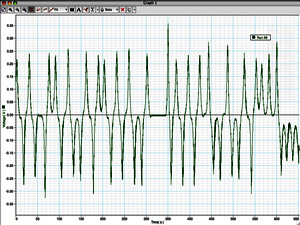
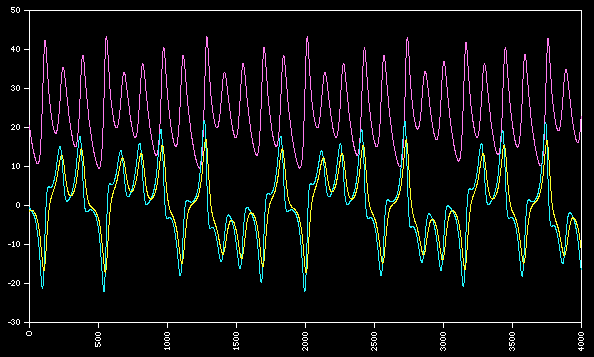
The lorenz attractor was first studied by Ed N. Lorenz, a meteorologist, around 1963. It was derived from a simplified model of convection in the earth's atmosphere. It also arises naturally in models of lasers and dynamos. The system is most commonly expressed as 3 coupled non-linear differential equations. dy / dt = x (b - z) - y dz / dt = xy - c z One commonly used set of constants is a = 10, b = 28, c = 8 / 3. Another is a = 28, b = 46.92, c = 4. "a" is sometimes known as the Prandtl number and "b" the Rayleigh number. The series does not form limit cycles nor does it ever reach a steady state. Instead it is an example of deterministic chaos. As with other chaotic systems the Lorenz system is sensitive to the initial conditions, two initial states no matter how close will diverge, usually sooner rather than later. Typical traces of each coordinate are shown below
While the equations look simple enough they lead to wondrous trajectories, some examples of which are illustrated below. 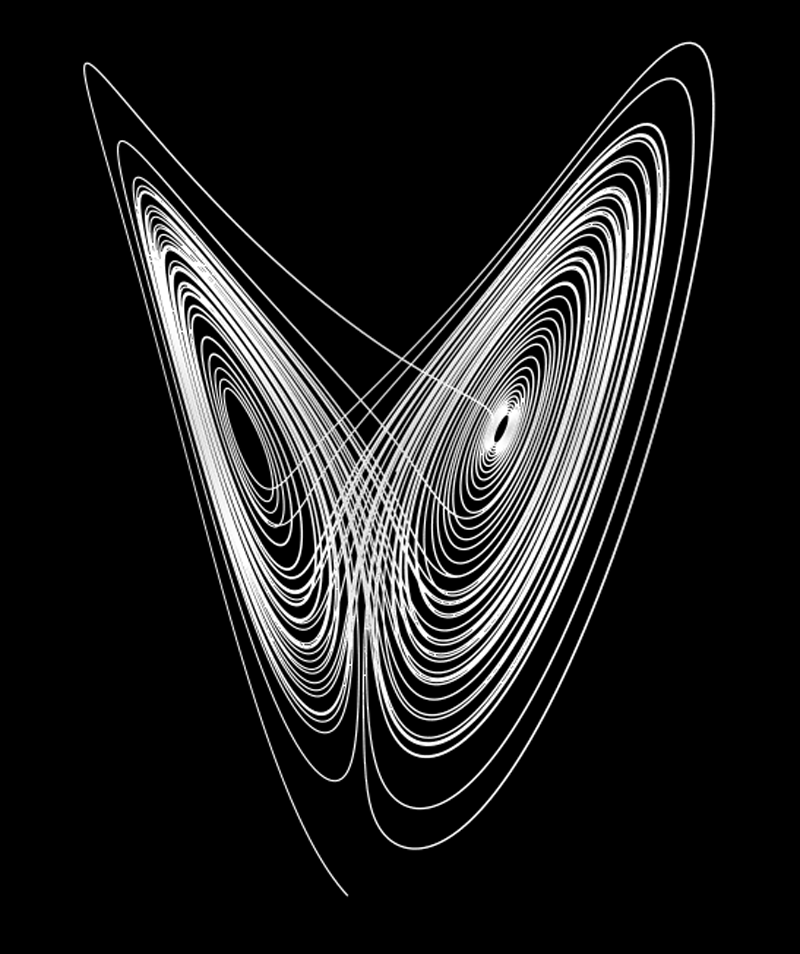 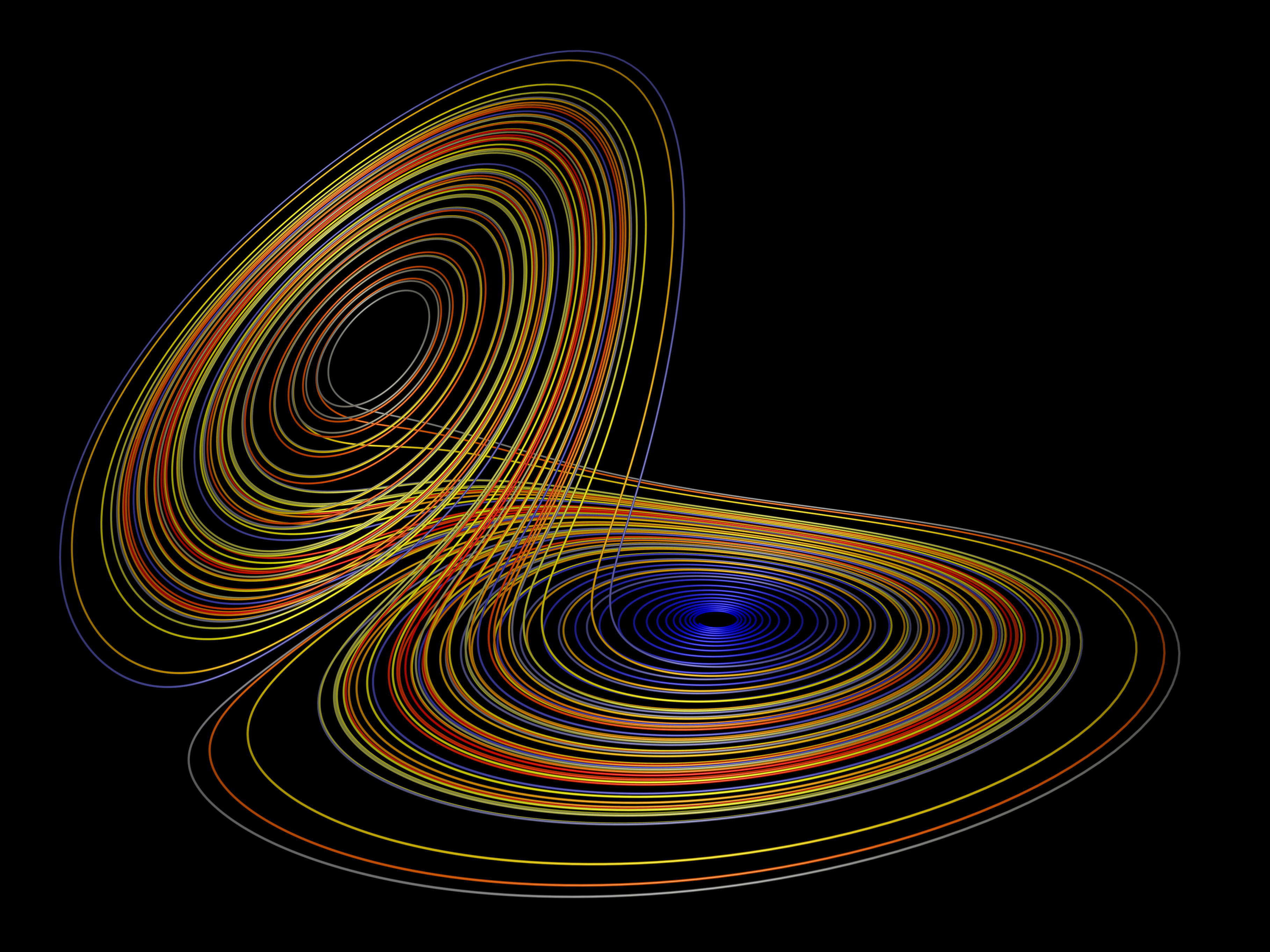 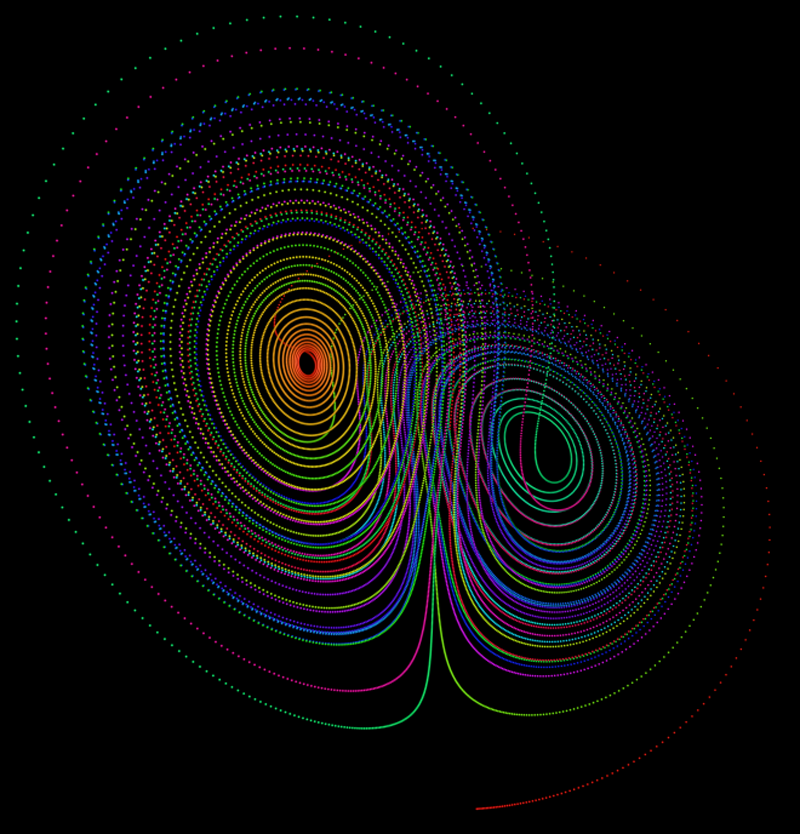 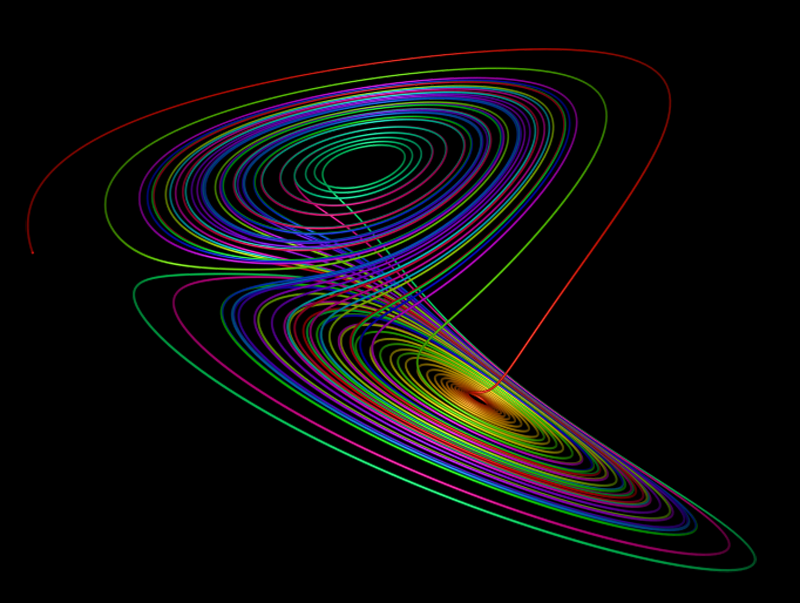 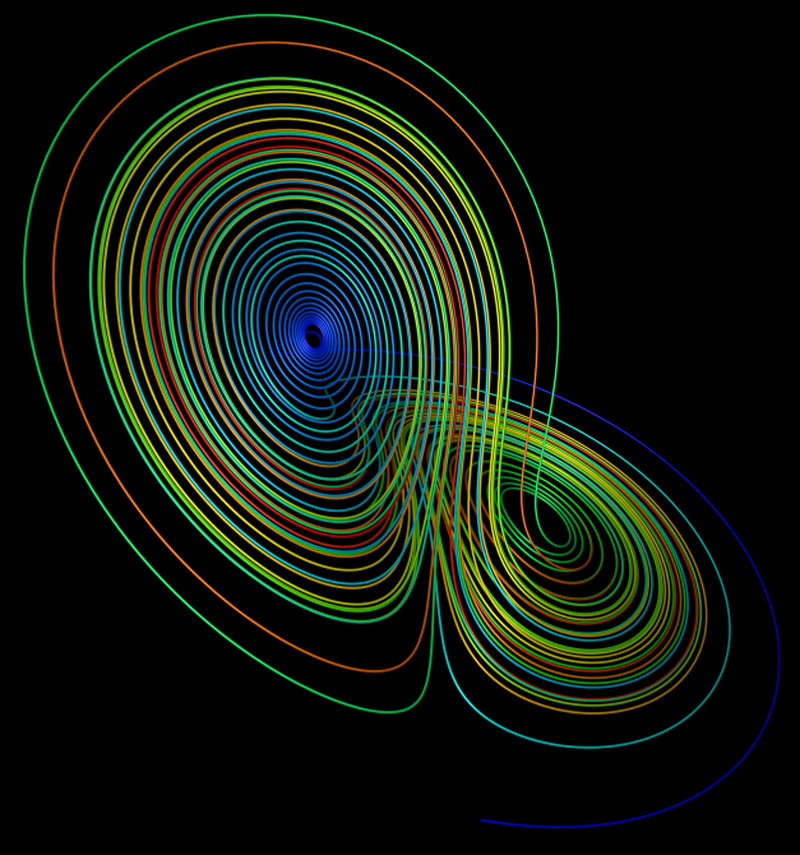 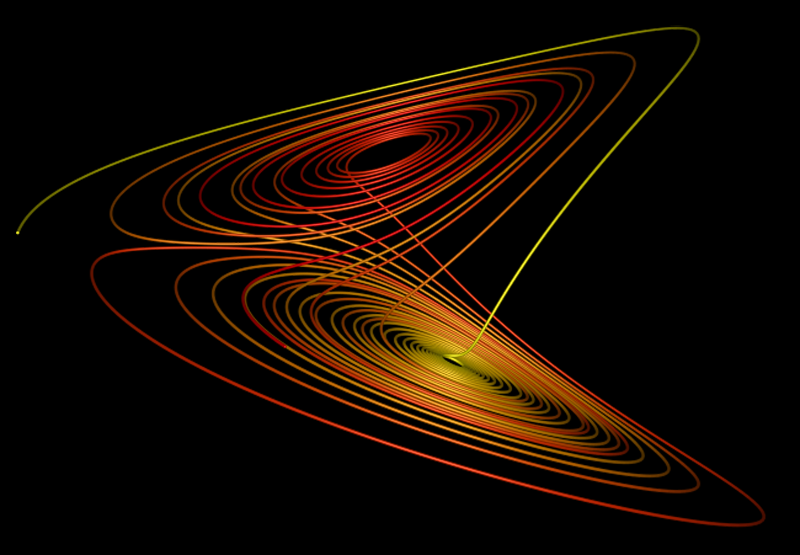 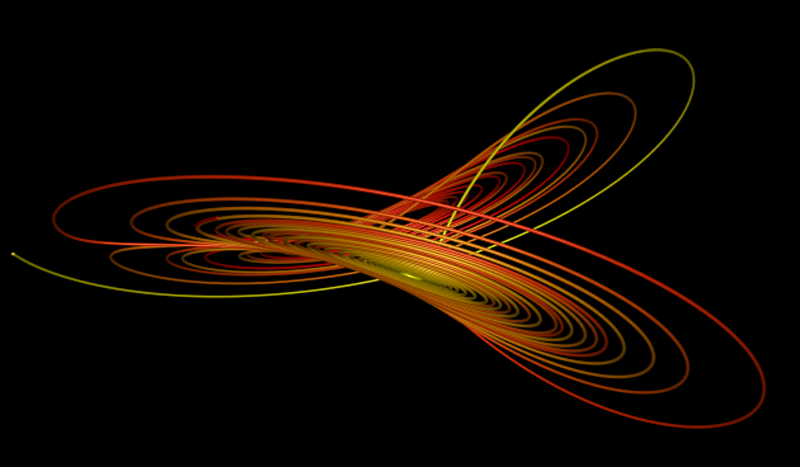 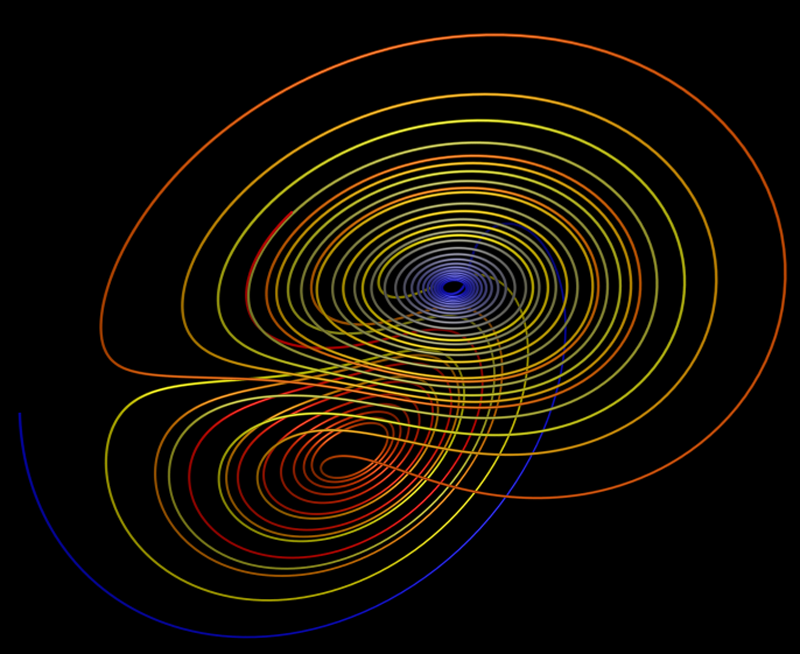 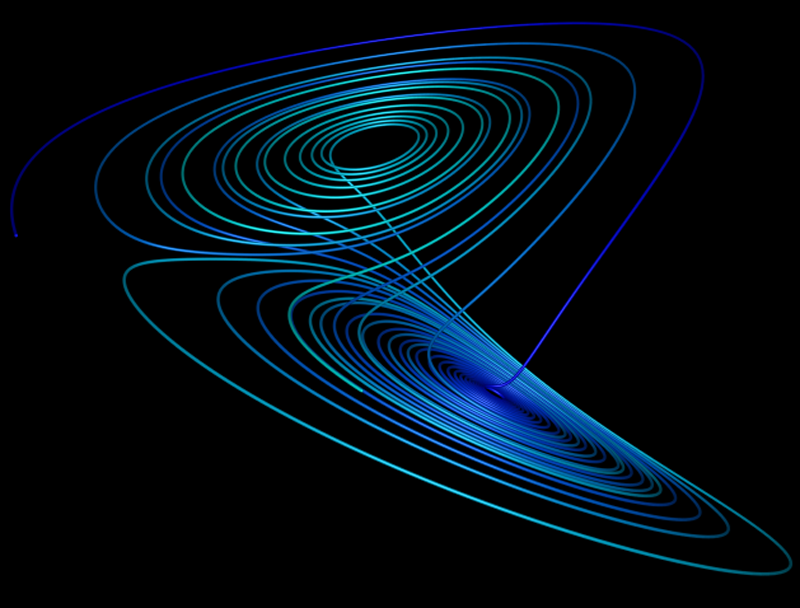

PovRay 3.5 macro by Marcus Fritzsch
// N = number iterations
// h, a, b, c: initial parameters
// x0, y0, z0: start-location
// rad = radius of the spheres that trace the attractor
#macro lorenz(h, a, b, c, x0, y0, z0, N, rad)
// use it like:
// lorenz(0.001099, 10, 28, 8/3, 0.0001, 0.0001, 0.0001, 350000, 0.04)
#local i = 0;
union {
#while (i < N)
#local x1 = x0 + h * a * (y0 - x0);
#local y1 = y0 + h * (x0 * (b - z0) - y0);
#local z1 = z0 + h * (x0 * y0 - c * z0);
#if (i > 100)
sphere {
<x0,y0,z0>, rad
pigment { color rgb <i/N,i/N,1> }
}
#end
#local i = i + 1;
#local x0 = x1;
#local y0 = y1;
#local z0 = z1;
#end
}
#end
PovRay rendering by Marcus Fritzsch 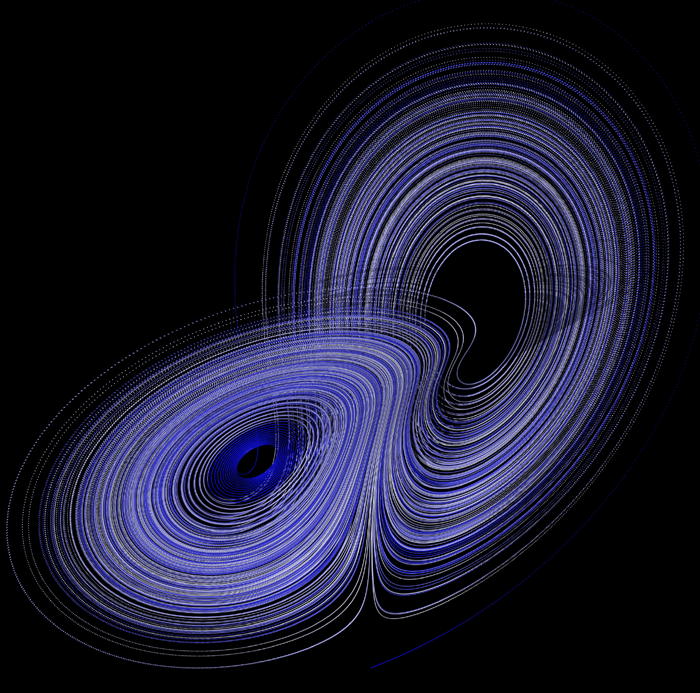
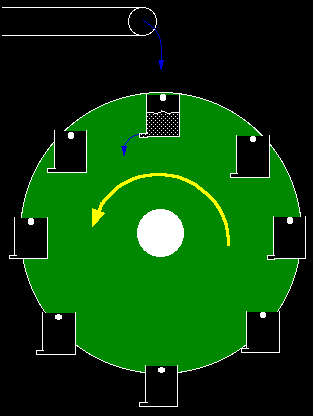
The waterwheel actually built by Planeten Paultje for the Dutch Annual Physics Teacher Conference in December 2005, the "Woudschotenconferentie Natuurkunde 2005".
Second Life example
default {
state_entry() {
llOwnerSay("Touch to start build");
}
touch_start(integer total_number) {
integer i;
integer N = 3000;
integer counter = 0;
float a = 10;
float b = 28;
float c = 8/3.0;
float h = 0.01;
vector p0 = <0.1,0,0>;
vector plast = p0;
vector p1;
vector offset = <0,0,-1>;
float scalefactor = 0.15;
offset += llGetPos();
for (i=0;counter<N;i++) {
p1.x = p0.x + h * a * (p0.y - p0.x);
p1.y = p0.y + h * (p0.x * (b - p0.z) - p0.y);
p1.z = p0.z + h * (p0.x * p0.y - c * p0.z);
llOwnerSay((string)i + " <" + (string)p1.x + "," + (string)p1.y + "," + (string)p1.z +">");
if (i > 100) {
//llRezObject("ball", p1+offset, ZERO_VECTOR, ZERO_ROTATION, 1);
rotation rot = llRotBetween(<0,0,1>,scalefactor*(p1-plast));
integer len = (integer)(100*llVecMag(scalefactor*(p1-plast)));
if (len > 10) {
llRezObject("lineseg", offset + scalefactor*(p1+plast)/2, ZERO_VECTOR, rot, len);
plast = p1;
counter++;
}
} else {
plast = p1;
}
p0 = p1;
}
}
}

 Sculpture in Vevey, Switzerland
|