Interlinked square toriWritten and visualisations by Paul Bourke. Inspiration, algorithm and geometry generated by John ShierJanuary 2014
The following is a continuation of the work by John Shier on so called "statistical geometry fractals" introduced here in one, two, and three dimensions and published in (1). The work presented here was inspired by a previously studied example in three dimensions using randomly orientated tori, of interest was the interlocking of the tori which was a natural consequence of the space filling process. 
In what follows, the tori are square and always axis aligned, this makes the intersection test between two square tori faster and it is imagined increases the chances of linkages. They are defined by a centroid, the plane they reside on (xy, yz, zx), their size, and the relative thickness of the tori cross-section. The cross-sectional relative thickness is constant during the space filling process. One effect of reducing the relative thickness of the tori cross section is that it increases the chance of linkages. Note there are equal numbers of tori on each plane, they are added to the space filling process in equal order. As a means of verifying the process the results were visualised in PovRay, this allowed visual confirmation that the space filling process was occurring as expected. When studying the linkages the same visualisation techniques could be used to verify tori that were supposed to be in a linked set were indeed all linked. In the following rendering the tori have a different material depending on the plane they are aligned to. The space filling process can be implemented with contained boundary conditions or periodic boundary conditions, the later is used here.  8000 tori, ignoring duplicates as part of the tiling unit The structure can be easier to interpret if the tori are drawn with circular cross-sections, this provides more shading information and due to the extra gaps allows one to see further into the interior. Note that this is purely a visual technique, the space filling was still performed as if the tori had the square profile.  The yellow/green frame shows the cubic space being filled The periodic boundary conditions means that the filled cube can tile space, a 3x3x1 tiling is illustrated below. 
In addition to the space filling process this work looked at the linkages between tori and additionally identifying large collections of linked tori. In the set shown above the following is the largest single set of linked tori, 835 in total. In case it isn't clear, this is a single connected object ... if it were a physical object then no individual tori could be separated from the group without a breakage. 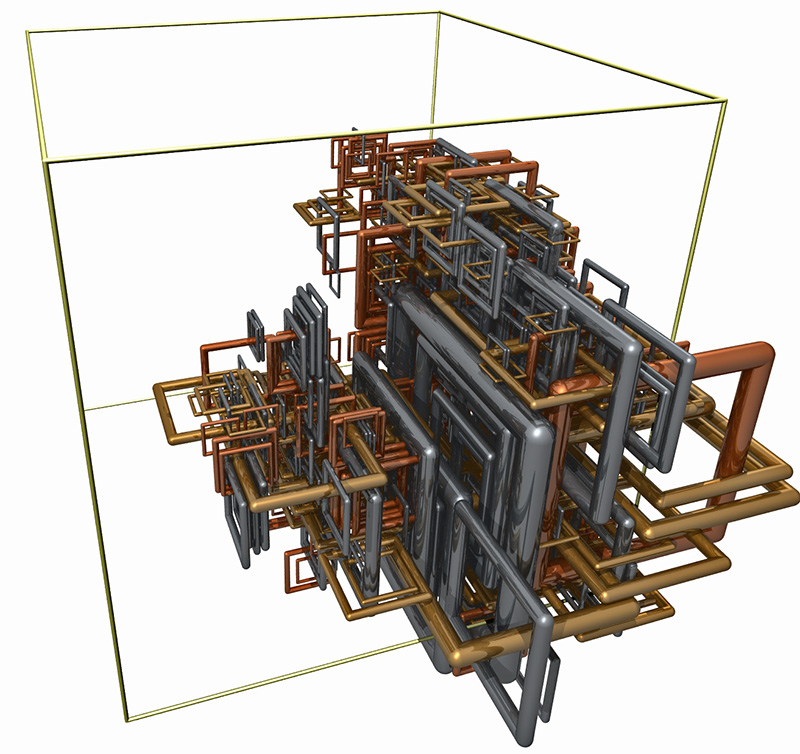
Another interesting way of visualising the results is to print a physical version of an interlinked set. This not only allows one to explore the object/data in the same way as we normally explore objects in real life (using our hands and eyes) but also confirms the set is a connected set by noticing that no tori "drop out". 
The physical object is strangely engaging due, it is proposed, to the mixture between order (the central tori that are constrained due to their density) and the messy disorder of the loose exterior strands the hang away from the main structure. 
As a small technical note on the 3D printing process, the current state of the technology has various constraints relating to colour fidelity, resolution, and the smallest structures that can be realised. The 3D prints shown here were performed on the ObJet printers since they, at the time of writing, were able to resolve the fine structures required for the smallest tori in the dataset. Unfortunately that printer does not support other than a single colour.  Model as it appears in the Shapeways 3D Printing service web site
(1) An Algorithm for Random Fractal Filling of Space, John Shier and Paul Bourke, Computer Graphics Forum, Vol. 32, Issue 8, pp. 89-97, December 2013. (2) A space filling algorithm for generating procedural geometry and texture. Paul Bourke. GSTF International Journal on Computing (JoC), Vol. 3, No. 2, 2013, pp 75-79. ISSN: 2251-3043. E-periodical: 2010-2283. DOI: 10.5176/2251-3043_3.2.260 (3) Space Filling: A new algorithm for procedural creation of (some) game assets. Paul Bourke, John Shier. Proceedings of the 6th Annual International Conference on Computer Games Multimedia & Allied Technology (CGAT 2013), pp 1-5. ISSN: 2251-1679. doi: 10.5716/2251-1679_CGAT13.01 |