 Julia Set Fractal (2D)Written by Paul BourkeJune 2001
See also: Julia set of sin(z)
The Julia set is named after the French mathematician Gaston Julia who investigated their properties circa 1915 and culminated in his famous paper in 1918. While the Julia set is now associated with a simpler polynomial, Julia was interested in the iterative properties of a more general expression, namely z4 + z3/(z-1) + z2/(z3 + 4 z2 + 5) + c.
The Julia set is now associated with those points z = x + iy
on the complex plane for which the series
zn+1 = zn2 + c does not tend
to infinity. c is a complex constant, one gets a different Julia
set for each c. The initial value z0 for the series
is each point in the image plane.
In the broader sense the exact form of the
iterated function may be anything, the general form being
zn+1 = f(zn), interesting sets arise
with non-linear functions f(z). Commonly used functions include
the following:
Computing a Julia set by computer is straightforward, at least by the brute force method presented here. The image is created by mapping each pixel to a rectangular region of the complex plane. Each pixel then represents the starting point for the series, z0. The series is computed for each pixel and if it diverges to infinity it is drawn in white, if it doesn't then it is drawn black. This convergence or otherwise isn't always obvious and it may take a large number of iterations to resolve so a decision procedure is required to determine divergence. This typically involves assuming the series tends to infinity as soon as its value exceeds some value, if the series hasn't diverged after a certain number of terms it is similarly assigned to be part of the set. Both these decisions can be varied to give more precise images but ones that take longer to calculate. An added effect is achieved by colouring the point by how fast it diverges to infinity. The well known Mandelbrot set forms a kind of index into the Julia set. A Julia set is either connected or disconnected, values of c chosen from within the Mandelbrot set are connected while those from the outside of the Mandelbrot set are disconnected. The disconnected sets are often called "dust", they consist of individual points no matter what resolution they are viewed at.  Another property of Julia sets relates to the various domains of c. If c is real then the Julia set is mirrored about the real axis. Other values of c with a non-zero imaginary component have 180 degree rotational symmetry.   c = 0 + 0.8i  c = 0.37 + 0.1i  c = 0.355 + 0.355i  c = -0.54 + 0.54i  c = -0.4 + -0.59i 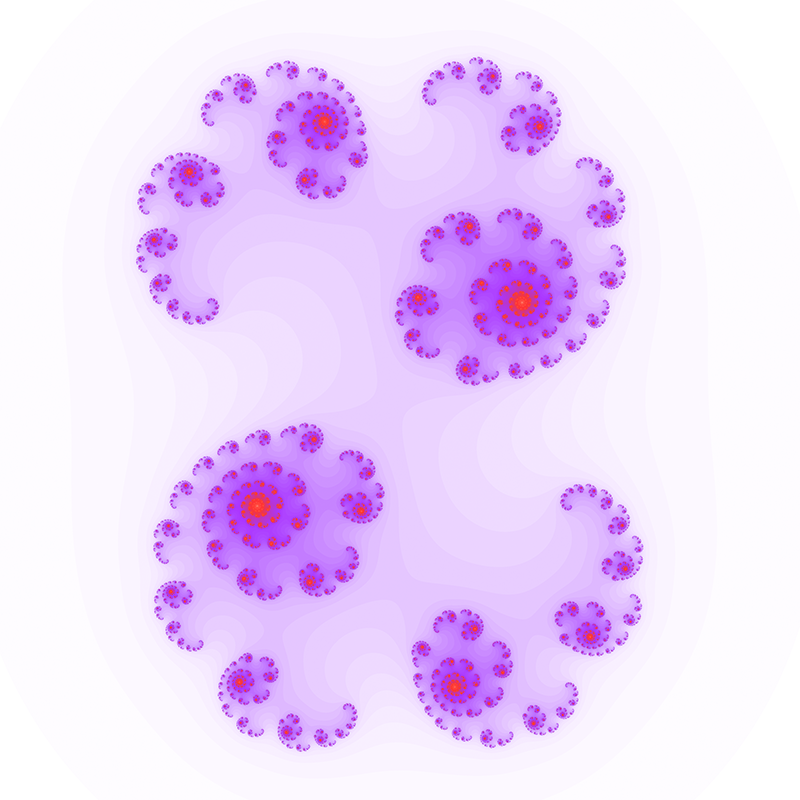 c = 0.34 + -0.05i  c = 0 + 0.8i  c = 0.37 + 0.1i  c = 0.355 + 0.355i 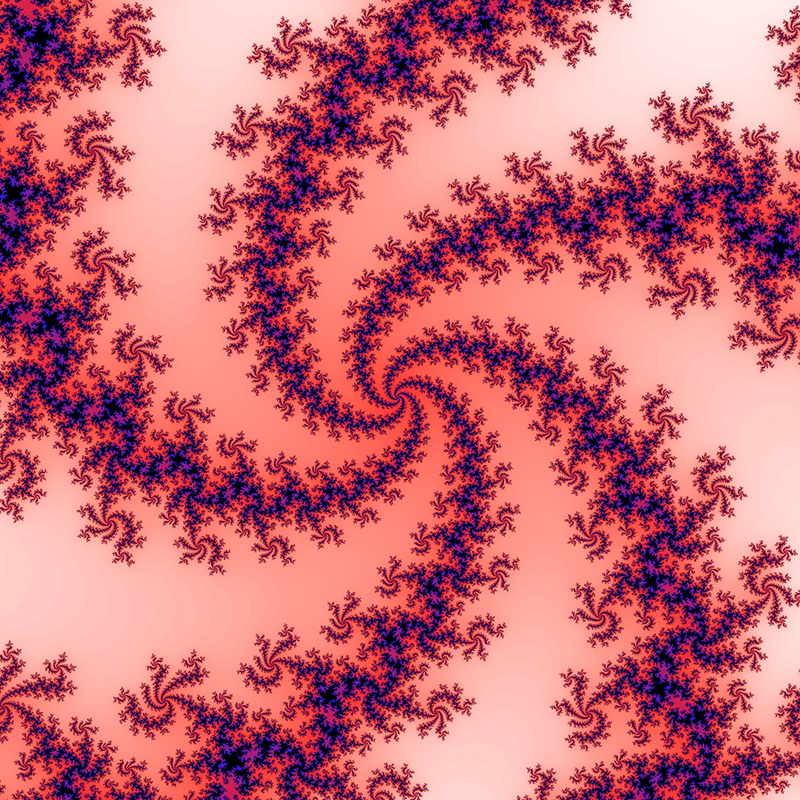 c = -0.54 + 0.54i  c = -0.4 + -0.59i  Value of c courtesy of Chris Thomasson c = 0.355534 - 0.337292i      Contributions by Klaus Messner
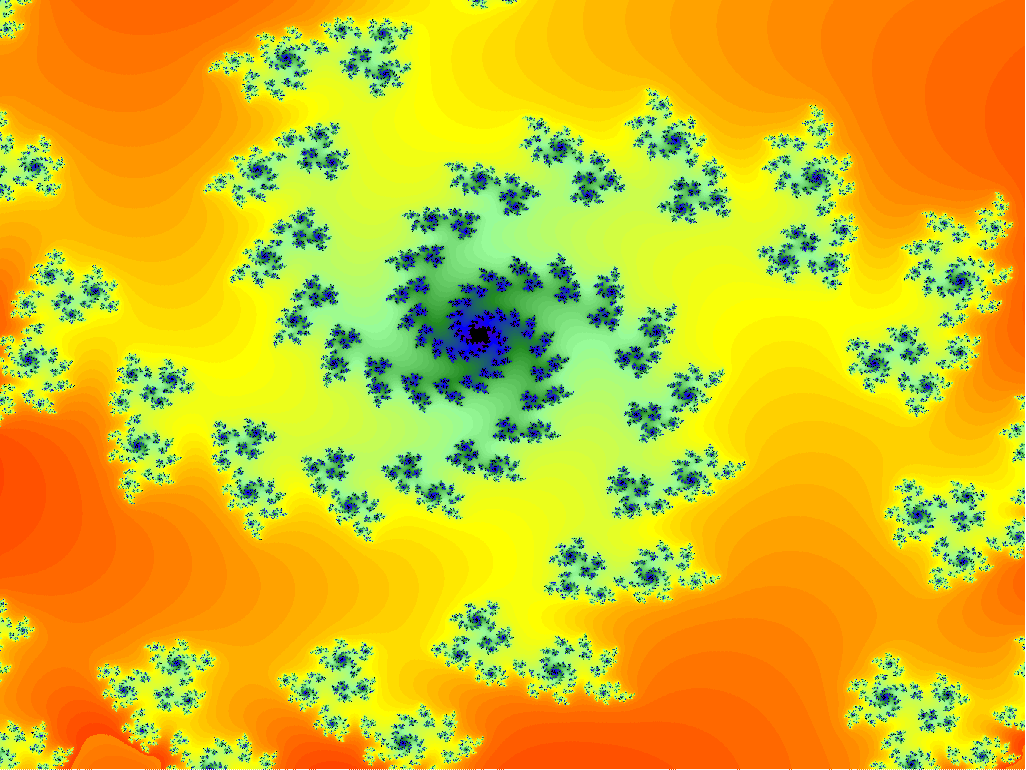 x = -0.202420806884766, y = 0.39527333577474
 x = -1.34882125854492, y = -0.454237874348958 |