Macintosh IFS manualWritten by Paul BourkeMay 1990
Introduction The following describes iterated function systems, a particular implementation on the Macintosh, and presents some examples. One of the many ways of describing the affine transformations for iterated functions systems (IFS) is as follows:
y = -r sin(theta) x + s cos(phi) y + k Generally there are a number of these mappings (different values of r, s, theta, phi, h, k) which are chosen at random at each iteration. How does the program work The fundamental iterative process involves replacing rectangles with a series of rectangles called the generator. The rectangles are replaced by a suitably scaled, translated, and rotated version of the generator. For example consider the generator below
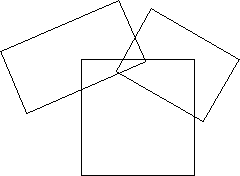 It consists of three rectangles, each with its own center, dimensions and rotation angle. The initial conditions usually consist of a single square, the first iteration then consists of replacing this square by a suitably positioned, scaled and rotated version of the above generator. The result would just be the generator above. The next iteration involves replacing each of the rectangles in the current system by suitabled positioned, scaled, and rotated versions of the generator resulting in the following 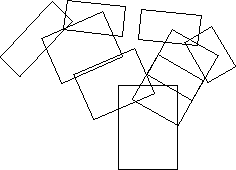 The next iteration replaces each rectangle above again by the initial generator as shown below 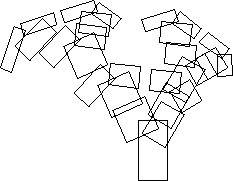 and so on, three iterations later  IFS allows the user to explore the result of applying different generators. The generator rectangles can be created, shifted, scaled, and rotated by the handles on each rectangle shown below. 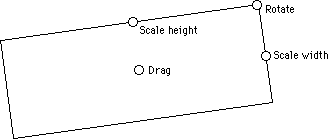 The user may iterate forward or in reverse, colour the borders, interior, or background. A library of interesting generators is provided for initial experimentation. Generators created by users may be saved in files and recalled at a later time. Images so created may be copied from IFS and pasted into a more standard drawing package for incorporation into a document and printing. Hopalong or "The Chaos Game" A technique exists by which the resulting form after an infinite number of iterations can be derived. This is a function of the form 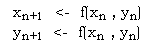 This gives a series of (x,y) points all which lie on the result of an infinite IFS. Although it still takes an infinite number of terms in this series to form the result the appearance can be readily appreciated after a modest number of terms (10000 say). 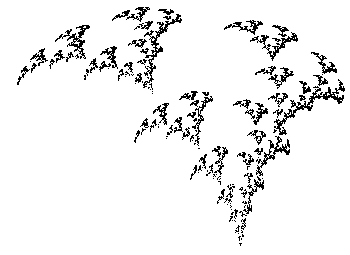 Note that with both methods it is possible to create the image at any scale. In many but not all cases zoomed in examples will be exhibit self similarity at all scales. Applications Data reduction for model files. If a generator can be found for a complex image then storing the generator and the rules of production results in a great deal of data reduction. For example the weed in the examples above might eventually contain over 2000 rectangles but is completely specified by the characteristics of 3 rectangles, only 5 numbers, center (cx,cy), scale (sx,sy), and angle Note: it is not necessarily trivial to derive a rectangular generator for an arbitrary form, although it is possible to create a polygonal generator for any form. The following shows a maple leaf generated using the IFS program. 
Some other IFS examples of plant-like structures are shown below
References Demko, S., Hodges, L., and Naylor B. Construction of Fractal Objects with Iterated Function Systems. Computer Graphics 19, 3, July 1985, Pages 271-278 Barnsley, M. Fractals Everywhere. Academic press, 1988 Barnsley, F., and Sloan, A.D. A Better Way to Compress Images. Byte Magazine, January 1988, Pages 215-222 Oppenheimer, P.E. Real Time Design and Animation of Fractal Plants and Trees. Computer Graphics, 20, 4, 1986 Reghbati, H.K. An Overview of Data Compression Techniques. Computer, 14, 4, 1981, Pages 71-76
Gallery of Randomly Generated IFSCreated by Paul BourkeMarch 1998 The following images are a selection from an infinite set of Random Iterated Function Systems (IFS) of the form
yn+1 = d xn + e yn + f
For the mapping to contractive the following must all be true.
b2 + e2 < 1 a2 + b2 + d2 + e2 < 1 + (ae - db)2 For any particular image there are 4 different sets of values for (a,b,c,d,e,f) all on the interval [-1,1]. At each iteration step one of the sets is chosen at random to form the next term in the sequence (series). The results fall into the following broad classes of images
The third "interesting" category can be further classified as follows
3D IFS Bush (weed)Written by Paul BourkeMay 2003 Original model from the authors of "IFS Builder 3d".

This bush is created by iteratively choosing one of the following functions at random to form a series pn. Each point in the series is represented as a small sphere, the final collection is rendered using PovRay. In order minimise the number of spheres to be rendered (IFS tend to require a very large number of points) the spheres are filtered such that no two spheres lie within 10% of their respective radii.
General N tile IFSInspired by Roger BagulaCompiled and graphics by Paul Bourke Original October 1998, images updated January 2018




Maple Leaf IFSWritten by Paul BourkeJanuary 2002
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3 set 4
a 0.1400 0.4300 0.4500 0.4900
b 0.0100 0.5200 -0.4900 0.0000
c 0.0000 -0.4500 0.4700 0.0000
d 0.5100 0.5000 0.4700 0.5100
e -0.0800 1.4900 -1.6200 0.0200
f -1.3100 -0.7500 -0.7400 1.6200

Features in the Diaorama Magazine, issue 4, May 2013. IFS SpiralWritten by Paul BourkeJanuary 2002
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3
a 0.787879 -0.121212 0.181818
b -0.424242 0.257576 -0.136364
c 0.242424 0.151515 0.090909
d 0.859848 0.053030 0.181818
e 1.758647 -6.721654 6.086107
f 1.408065 1.377236 1.568035
probability 0.90 0.05 0.05
IFS Mandelbrot-likeWritten by Paul BourkeFebruary 1999
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2
a 0.2020 0.1380
b -0.8050 0.6650
c -0.6890 -0.5020
d -0.3420 -0.2220
e -0.3730 0.6600
f -0.6530 -0.2770
IFS TreeWritten by Paul BourkeJanuary 1999
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3 set 4 set 5 set 6 set 7
a 0.0500 -0.0500 0.0300 -0.0300 0.5600 0.1900 -0.3300
b 0.0000 0.0000 -0.1400 0.1400 0.4400 0.0700 -0.3400
c 0.0000 0.0000 0.0000 0.0000 -0.3700 -0.1000 -0.3300
d 0.4000 -0.4000 0.2600 -0.2600 0.5100 0.1500 0.3400
e -0.0600 -0.0600 -0.1600 -0.1600 0.3000 -0.2000 -0.5400
f -0.4700 -0.4700 -0.0100 -0.0100 0.1500 0.2800 0.3900

Derby, Western Australia
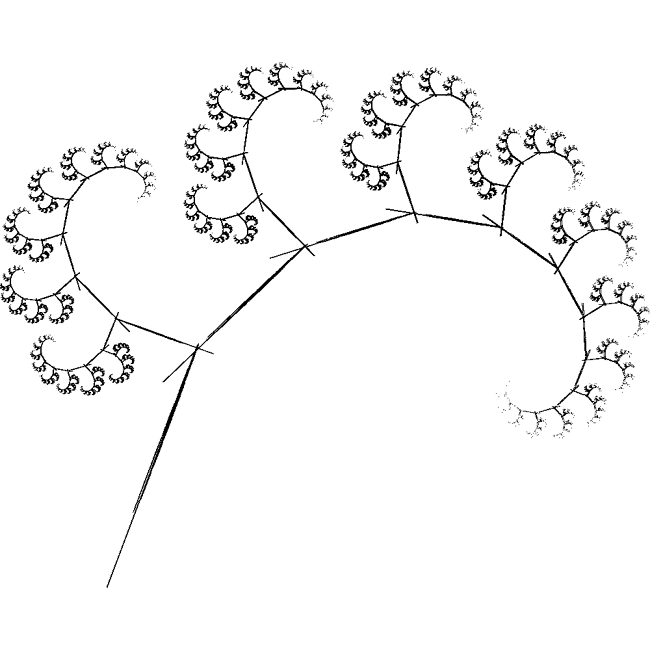
IFS TreeWritten by Paul BourkeJanuary 1999
 The IFS equations are as follows yn+1 = r sin(theta) xn + s cos(phi) yn + f
set 1 set 2 set 3 set 4 set 5 set 6
r 0.0500 0.0500 0.6000 0.5000 0.5000 0.5500
s 0.6000 -0.5000 0.5000 0.4500 0.5500 0.4000
theta 0.0000 0.0000 0.6980 0.3490 -0.5240 -0.6980
phi 0.0000 0.0000 0.6980 0.3492 -0.5240 -0.6980
e 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
f 0.0000 1.0000 0.6000 1.1000 1.0000 0.7000
IFS TreeWritten by Paul BourkeJanuary 1999
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3 set 4
a 0.0100 -0.0100 0.4200 0.4200
b 0.0000 0.0000 -0.4200 0.4200
c 0.0000 0.0000 0.4200 -0.4200
d 0.4500 -0.4500 0.4200 0.4200
e 0.0000 0.0000 0.0000 0.0000
f 0.0000 0.4000 0.4000 0.4000
IFS TreeWritten by Paul BourkeJanuary 1999
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3 set 4 set 5
a 0.1950 0.4620 -0.6370 -0.0350 -0.0580
b -0.4880 0.4140 0.0000 0.0700 -0.0700
c 0.3440 -0.2520 0.0000 -0.4690 0.4530
d 0.4430 0.3610 0.5010 0.0220 -0.1110
e 0.4431 0.2511 0.8562 0.4884 0.5976
f 0.2452 0.5692 0.2512 0.5069 0.0969
probability 0.2 0.2 0.2 0.2 0.2
Leaf IFSWritten by Paul BourkeJanuary 2002
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3 set 4
a 0.0000 0.7248 0.1583 0.3386
b 0.2439 0.0337 -0.1297 0.3694
c 0.0000 -0.0253 0.3550 0.2227
d 0.3053 0.7426 0.3676 -0.0756
e 0.0000 0.2060 0.1383 0.0679
f 0.0000 0.2538 0.1750 0.0826
Sand dollar snowflake IFSWritten by Paul BourkeJanuary 2002
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3 set 4 set 5 set 6
a 0.38200 0.11800 0.11800 -0.30900 -0.30900 0.38200
b 0.00000 -0.36330 0.36330 -0.22450 0.22450 0.00000
c 0.00000 0.36330 -0.36330 0.22450 -0.22450 0.00000
d 0.38200 0.11800 0.11800 -0.30900 -0.30900 -0.38200
e 0.30900 0.36330 0.51870 0.60700 0.70160 0.30900
f 0.57000 0.33060 0.69400 0.30900 0.53350 0.67700
How to create the IFS FernWritten by Paul BourkeJanuary 1988
See also

The image is self similar at all scales, one can zoom in as far as one wishes and the fronds will continue to resolve themselves. For example, the following image is a zoom in by 50. Note however that it takes an ever increasing number of iterations to resolve the image as the zoom factor increases, this image took 100 million (108) iterations. 
Some straightforward C source is given here (source.c) which generates the figure shown above. Note, you will have to supply your own image drawing tools.
 References Demko, S., Hodges, L., and Naylor B. Construction of Fractal Objects with Iterated Function Systems. Computer Graphics 19, 3, July 1985, Pages 271-278 Barnsley, M. Fractals Everywhere. Academic press, 1988 Barnsley, F., and Sloan, A.D. A Better Way to Compress Images. Byte Magazine, January 1988, Pages 215-222 >Oppenheimer, P.E. Real Time Design and Animation of Fractal Plants and Trees. Computer Graphics, 20, 4, 1986 Reghbati, H.K. An Overview of Data Compression Techniques. Computer, 14, 4, 1981, Pages 71-76
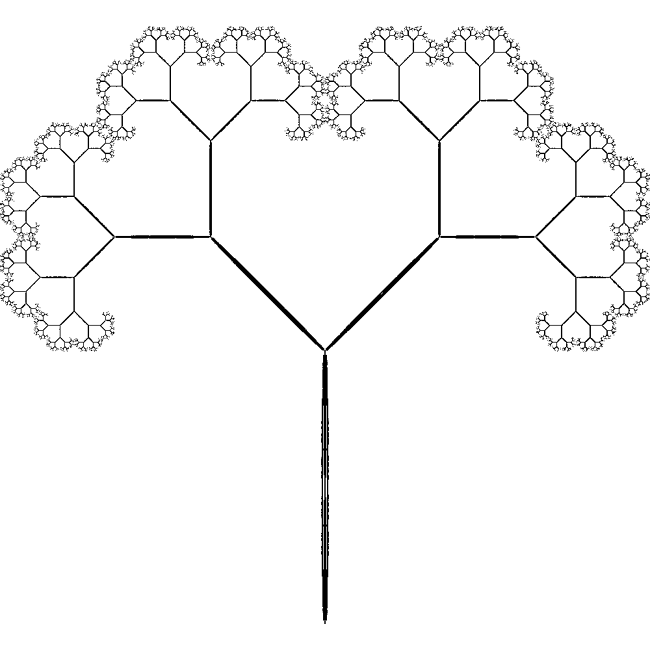
IFS fernWritten by Paul BourkeJanuary 1999
 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3
a 0.0100 0.7000 0.0000
b -0.4100 0.3300 0.1750
c 0.3900 -0.3500 0.0130
d 0.0000 0.7000 0.4600
e -0.2800 0.1850 -0.0950
f -0.1850 0.0150 -0.2850
IFS Chaos TextWritten by Paul BourkeJanuary 2002 Contributed by Earl Glynn (Original source unknown)
The following is a rather unusual example of an iterated function system (IFS) that involves choosing at random one of 19 transformations of the form yn+1 = c xn + d yn + f
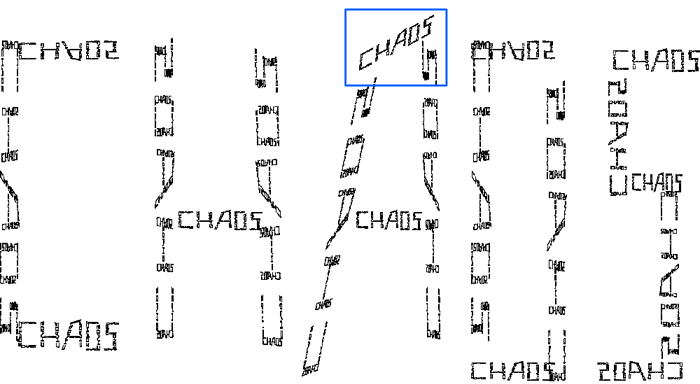
A zoom into the top portion of the "A", shown in blue above, shows that it is indeed made up of smaller versions of the word "chaos". 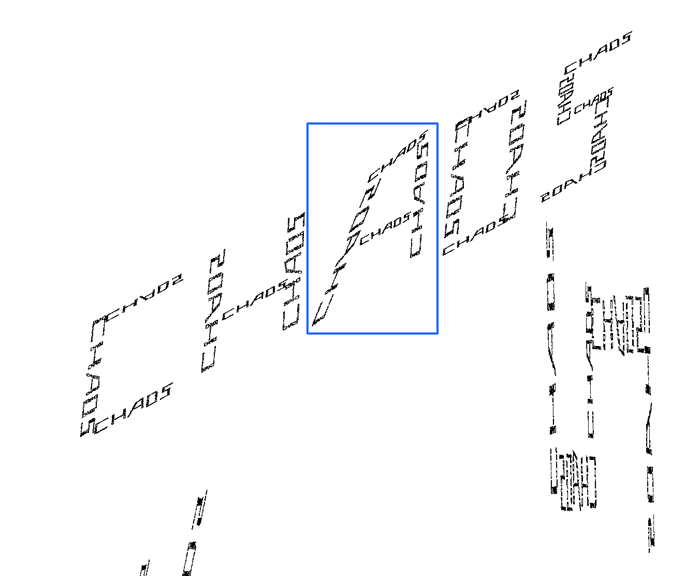
And to labour the point, the following is a further zoom into the "A", shown in blue above. 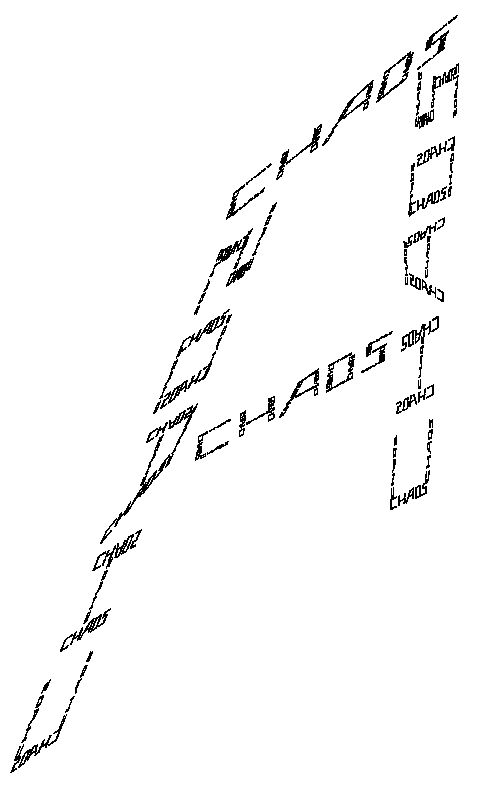 The parameter table:
a b c d e f
0 0.053 -0.429 0 -7.083 5.43
0.143 0 0 -0.053 -5.619 8.513
0.143 0 0 0.083 -5.619 2.057
0 0.053 0.429 0 -3.952 5.43
0.119 0 0 0.053 -2.555 4.536
-0.0123806 -0.0649723 0.423819 0.00189797 -1.226 5.235
0.0852291 0.0506328 0.420449 0.0156626 -0.421 4.569
0.104432 0.00529117 0.0570516 0.0527352 0.976 8.113
-0.00814186 -0.0417935 0.423922 0.00415972 1.934 5.37
0.093 0 0 0.053 0.861 4.536
0 0.053 -0.429 0 2.447 5.43
0.119 0 0 -0.053 3.363 8.513
0.119 0 0 0.053 3.363 1.487
0 0.053 0.429 0 3.972 4.569
0.123998 -0.00183957 0.000691208 0.0629731 6.275 7.716
0 0.053 0.167 0 5.215 6.483
0.071 0 0 0.053 6.279 5.298
0 -0.053 -0.238 0 6.805 3.714
-0.121 0 0 0.053 5.941 1.487
IFS DragonWritten by Paul BourkeJanuary 2002
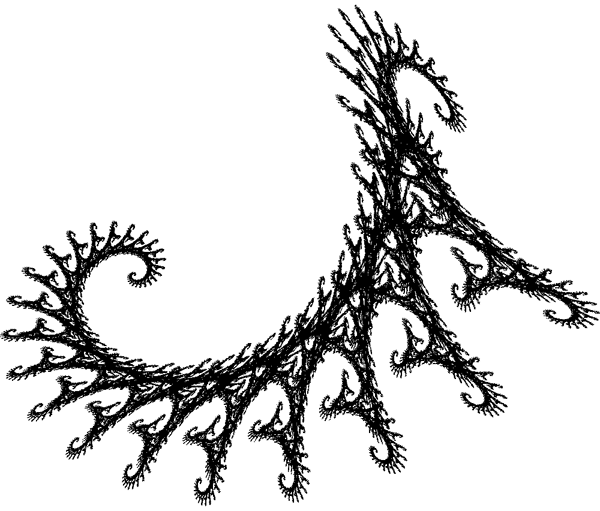 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2
a 0.824074 0.088272
b 0.281428 0.520988
c -0.212346 -0.463889
d 0.864198 -0.377778
e -1.882290 0.785360
f -0.110607 8.095795
probability 0.8 0.2

IFS TwigWritten by Paul BourkeJanuary 2002
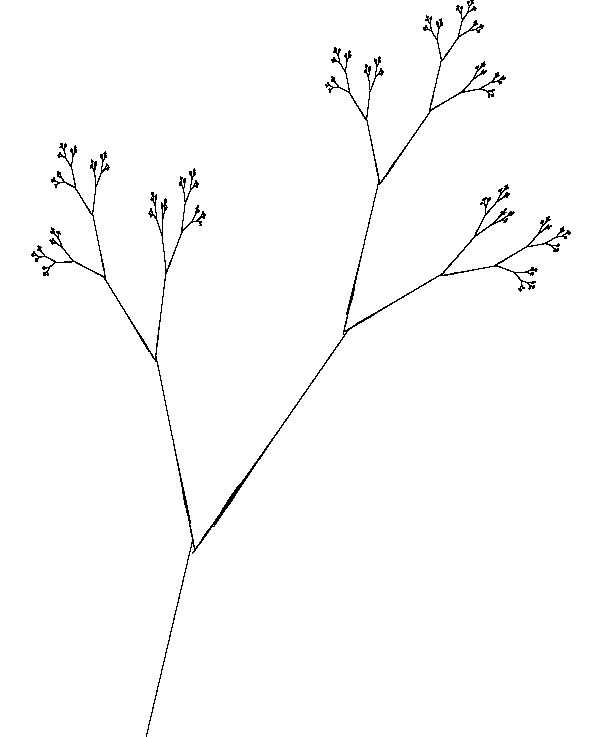 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3
a 0.387 0.441 -0.468
b 0.430 -0.091 0.020
c 0.430 -0.009 -0.113
d -0.387 -0.322 0.015
e 0.2560 0.4219 0.4
f 0.5220 0.5059 0.4
probability 1/3 1/3 1/3
Christmas tree IFSWritten by Paul BourkeJanuary 2002
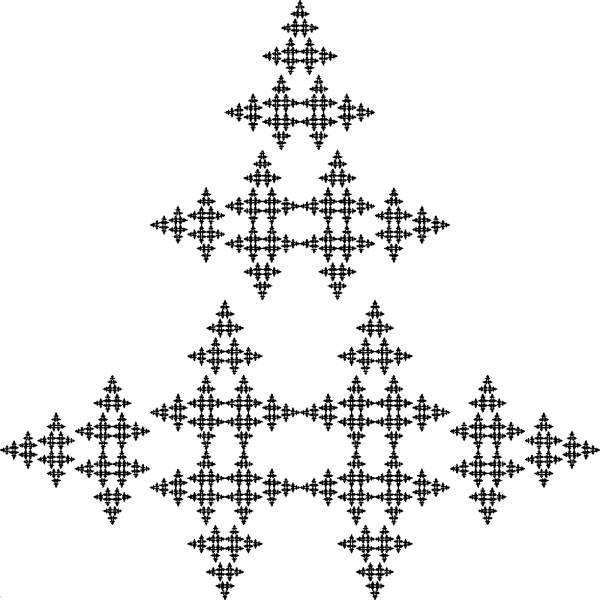 The IFS equations are as follows yn+1 = c xn + d yn + f
set 1 set 2 set 3
a 0.0 0.0 0.5
b -0.5 0.5 0.0
c 0.5 -0.5 0.0
d 0.0 0.0 0.5
e 0.5 0.5 0.25
f 0.0 0.5 0.5
probability 1/3 1/3 1/3
3D IFS HedgehogWritten by Paul BourkeMay 2003 Name attributed to the authors of "IFS Builder 3d".
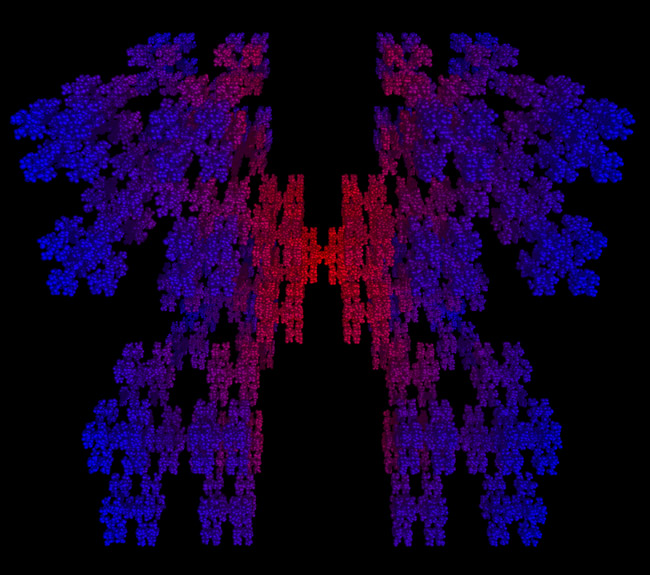
This beast is created by iteratively choosing one of the following functions at random to form a series pn. Each point in the series is represented as a small sphere, the final collection is rendered using PovRay. In order minimise the number of spheres to be rendered (IFS tend to require a very large number of points) the spheres are filtered such that no two spheres lie within 10% of their respective radii.
where a = (1 + 1/3) / 2 and b = (1 - 1/3) / 2
3D IFS CrossWritten by Paul BourkeMay 2003

This beast is created by iteratively choosing one of the following functions at random to form a series pn. Each point in the series is represented as a small sphere, the final collection is rendered using PovRay. In order minimise the number of spheres to be rendered (IFS tend to require a very large number of points) the spheres are filtered such that no two spheres lie within 10% of their respective radii.
where a = (1 + 1/3) / 2 and b = (1 - 1/3) / 2
|






















