Google Earth fractalsWritten by Paul BourkeStarted: October 2010. Last updated: October 2012
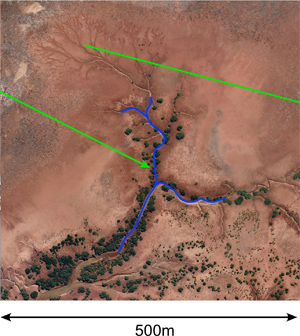
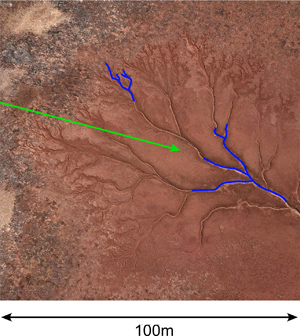
Introduction The following is a "photographic" gallery of fractal patterns found while exploring the planet with Google Earth. Each is provided with a KMZ file so the reader can explore the region for themselves. Readers are encouraged to submit their own discoveries for inclusion, credits will be included. Besides being examples of self similar fractals, they are often very beautiful structures ... not an uncommon characteristic of fractal geometry. Self Similarity Fractals are usually associated with self similarity across scales. For pure/idealised mathematical fractals the self similarity may be across an infinite range of scales, such as the Sierpinski Gasket. In real life and in nature the self similarity is only across a range of scales. Branching structures, such as most of the examples shown here, are classic examples of self similarity across 2, 3 or 4 scales. As with many plants, a thick branch (trunk) branches into one or more smaller branches, which in turn split into one or more smaller branches, and so on. The structure is similar at each scale, from the twigs to the main tree trunk. An example of this for a river system is illustrated below [KMZ file], clicking on an image will give the high resolution version of the image without the markings. For the image on the right the pixel size is 30cm, the image on the right has a pixel size of 7.5cm. At each scale the branching structures are similar in appearance. [Warning: the full size images are large.]
Another way to think about whether something exhibits self similarity is if it can be interpreted to exist at different scales. Consider the two images below, they can be imagined to be perhaps a stone of a few centimeters wide, a meter wide if imagined to be a rock face, or in the case of a mountain they may be a few kilometers wide.
| ||||||
| The Gallery | ||||||
|
Egypt: KMZ file

 New capture in March 2019
 | ||||||
|
South Korea: KMZ file
 | ||||||
|
Malaysia: KMZ file
 | ||||||
| ||||||
|
Australia: KMZ file



 | ||||||
|
Austria: KMZ file
 | ||||||
| ||||||
|
Spain: KMZ file: courtesy Aurelio Garcia.

 Spain: KMZ file courtesy of Eduardo Sáenz de Cabezón.
 Spain: KMZ file courtesy of Juan Luis Varona.

 | ||||||
|
Canada: KMZ file
 | ||||||
|
Canada: KMZ file courtesy Richard Thomson.
 | ||||||
|
Greenland: KMZ file
 | ||||||
|
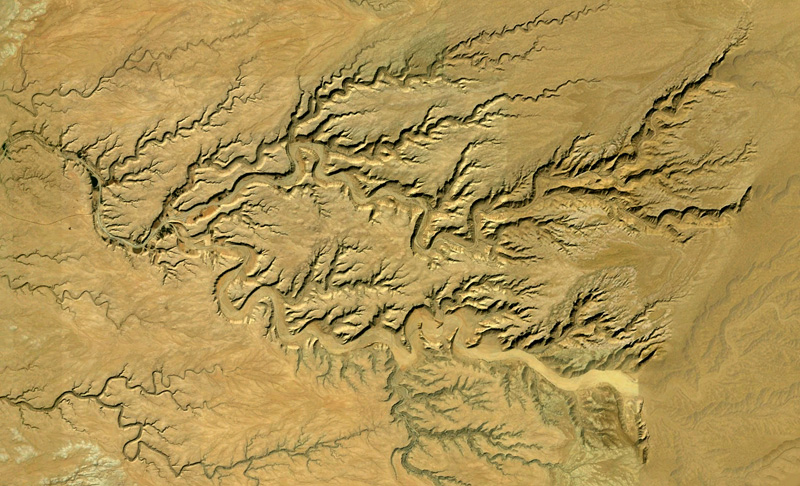
Saudi Arabia: KMZ file
 | ||||||
| ||||||
|
Algeria: KMZ file

 Features in the Diaorama Magazine, issue 4, May 2013. | ||||||
|
United States of America: KMZ file
 United States of America: KMZ file
 United States of America: KMZ file
 United States of America: KMZ file
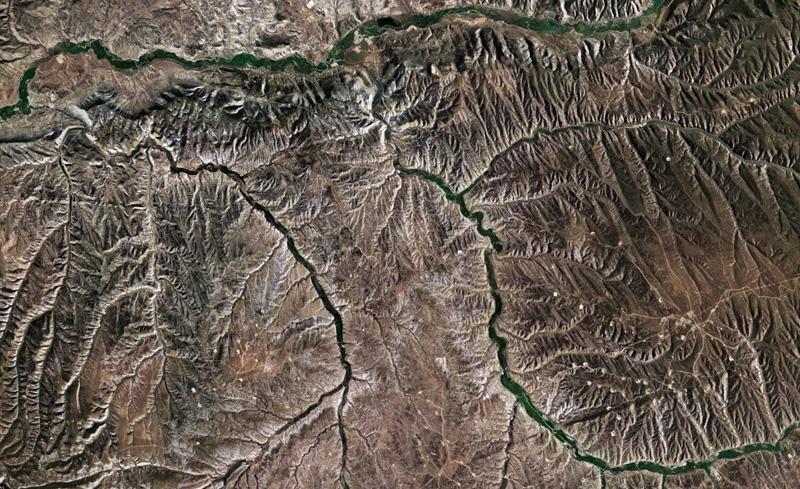 United States of America: KMZ file
 United States of America: KMZ file. courtesy of Emiel Boer.
 | ||||||
|
Norway: KMZ file
 | ||||||
| ||||||
|
Alaska: KMZ file


 | ||||||
|
Russia: KMZ file
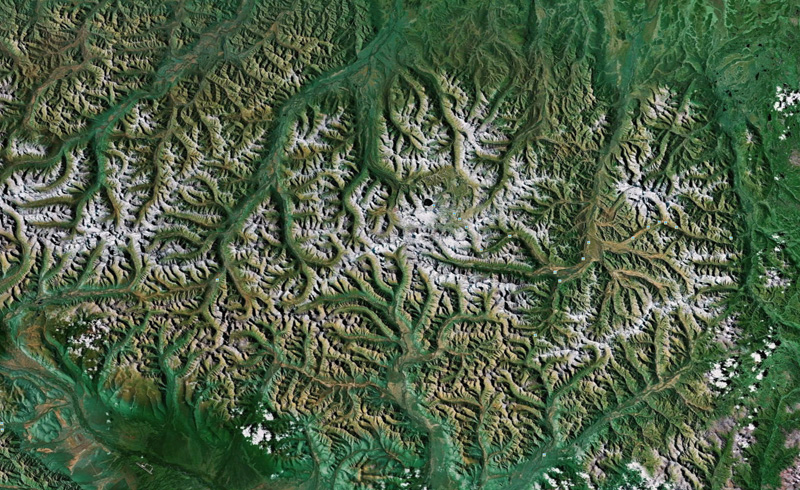
 | ||||||
|
China: KMZ file
 | ||||||
|
Afghanistan: KMZ file
 | ||||||
|
Burma: KMZ file
 Features in the Diaorama Magazine, issue 4, May 2013. | ||||||
| ||||||
|
India: KMZ file
 | ||||||
|
Laos: KMZ file
 | ||||||
|
Mexico: KMZ file
 | ||||||
|
South Africa: KMZ file
 | ||||||
|
Namibia: KMZ file
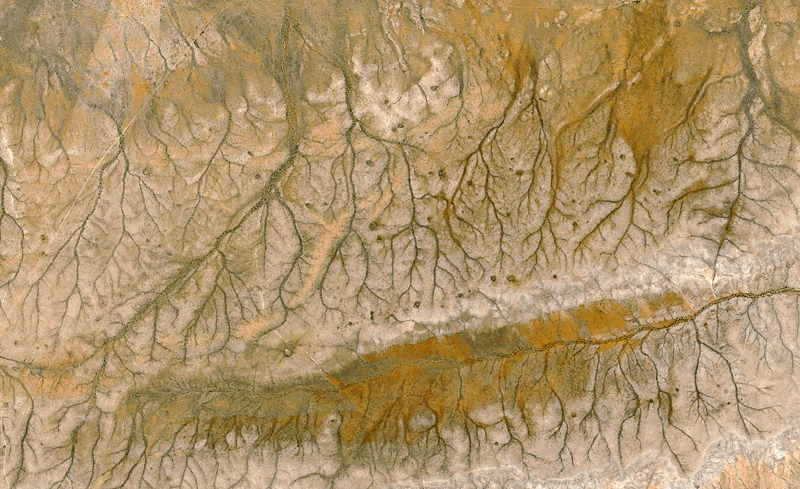
 | ||||||
|
Angola: KMZ file courtesy Pan Wolff.
 | ||||||
|
Colombia: KMZ file courtesy Fernando de Paz.
 | ||||||
|
Switzerland: KMZ file courtesy Lorant Buntye.
 | ||||||
| ||||||
|
Venezuela: KMZ file courtesy Fernando de Paz.
 | ||||||
|
Antarctica: KMZ file.
 | ||||||
|
Tibet: KMZ file.
 | ||||||
|
NearMap
There are mapping techniques that give higher resolution than Google Earth, namely aerial photography based upon surveys by planes or helicopters. Higher resolution in general would allow one to explore self similarity to smaller scales, that is, across a wider range of scales. The following examples are from an Australian product called NearMap, note that the sample areas tend to be on the coast and this is reflected in the examples presented.
|