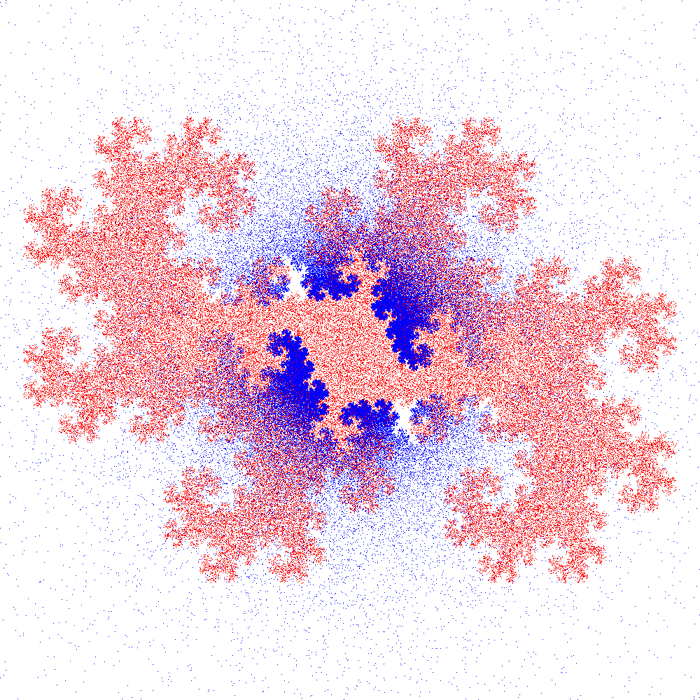
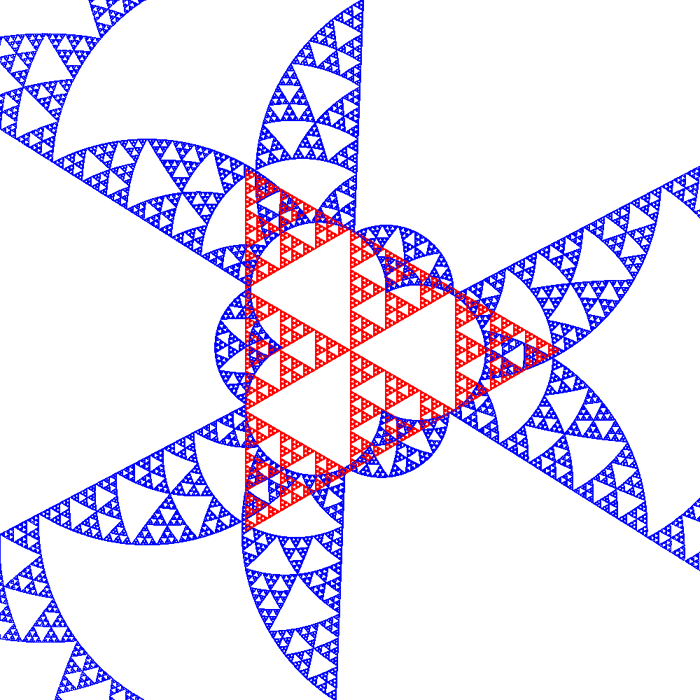
Experimental Orthogonal Fields to Sierpinski Sets and Twin DragonsBy Roger BagulaCompiled and graphics by Paul Bourke 5 Aug 1998

The theory of orthogonal fractal fields is that these sets depend on the dimensional self similarity of the fractal . Just how the dimensionality affects the orthogonality relationship is not an easy question. I have found a relationship that seems to give the desired orthogonal sets. The procedure is more of a monitor since it everywhere depends on the original fractal set: it is not an independent fractal. The equations are very simple:1) M = {{x,y},{xs,ys}} 2) determinant [M] = 1 - ds ( cross product) 3) (x,y) dot product (xs,ys) = x * xs + y * ys = ds It was finding a ds that gave a size and orientation that was orthogonal to the original set that is the experimental element. I tried a lot of combinations, but the following relationship gives the best output: 4) ds = 1 - 1 / s: 1 <= s <= s(Max)where s is the Moran similarity dimension for the fractal. Since in harmonic functions, the orthogonal relations also produce the derivatives, the solutions: 5) ys = (y * ds - x * (1 - ds)) / (x^2 + y^2)6) xs = -y * ys / x + ds / x can be called the fractal derivatives of the fractal functions. As I said before, they are not independent functions. The (ds,1 - ds) seem to be probabilities. If so this relationship can only work when s is greater than one. In three dimensions the equations are:7) M = {{x,y,z},{xs,ys,zs},{iv,jv,kv}} 8) det[M] = a * iv + b * jv + c * kv 9) sqr(a^2 + b^2 + c^2) = 1 - ds 10) x * xs + y * ys + z * zs = ds Suppose you had a 3d strange attractor whose Hausdorff dimension is known, then this kind of relationship determines a second strange attractor that is dependent on the first and is fractally orthogonal to the first. In terms of signalling and coding such orthogonality can be very useful. In the three dimensional case the nature of the root equations will give more than one solution to the above equations in most cases. Suppose you have tuned Chua oscillators in chaotic mode that are being used to encode a transmission: the orthogonality relationship would allow as many as three messages to be sent orthogonally at the same time. To an ordinary receiver the signals would appear to be noise. I state this idea here as a demonstration of the usefulness of fractal field theory in practical terms. Since these fields also have scaling orthogonality properties by their self similarity, image compression types of coding like with wavelets may also be a result of this mathematics. The twin dragon results seem to suggest a new dragon that is orthogonal to the twin dragon with an inner border that is itself a dragon. The relationship of the twin dragon to dualistic logic and fuzzy set analysis makes this result very interesting in theoretical terms. The exterior border to the orthogonal set is not as deterministic as one would expect. The relationship of the Cantor set to the Sierpinski gasket set seems important in fractal field orthogonality terms. It suggests some experiments in intersections and unions of fractal sets. That we don't know everything about fractals and how they work, doesn't mean that we aren't developing the science in very useful directions. A new definition of a fractal derivative that is independent of traditional calculus methods is also suggested by this line of research.
|