Duffing AttractorWritten by Paul BourkeMarch 1998 Listen (m4a or midi) to the Duffing attractor, the x and y values are sonified as two instruments. The solution to the Duffing equations is often used as an example of a classic chaotic system. The Duffing system of differential equations is
dy / dt = x - x3 - a y + b cos(w t) where typically, a = 0.25, b = 0.3, w = 1 The following shows a "typical" segment of (x,y) values. 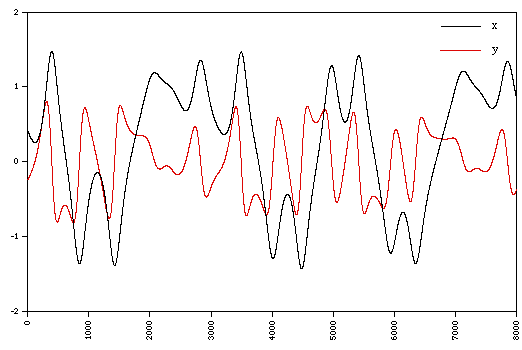 A longer sequence of the x variable is
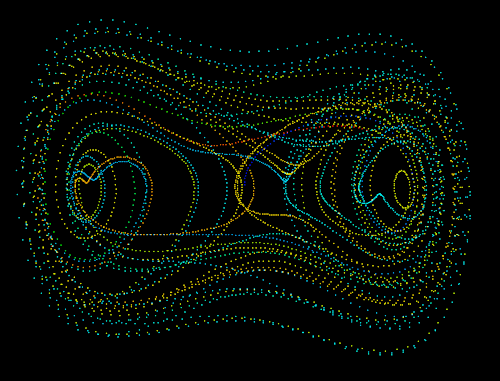
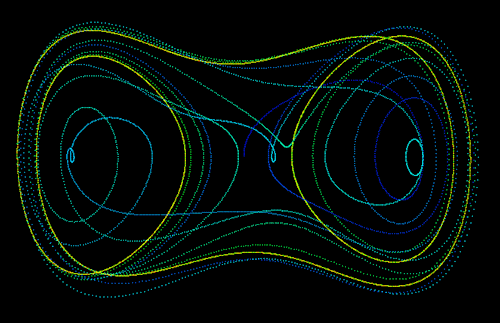
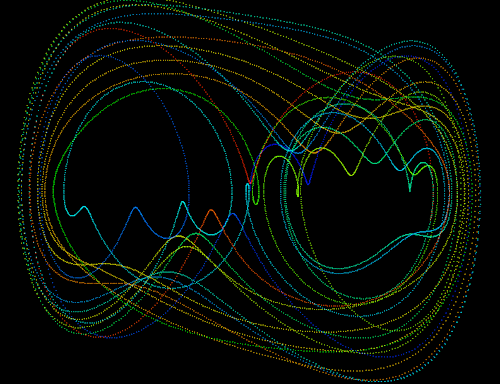
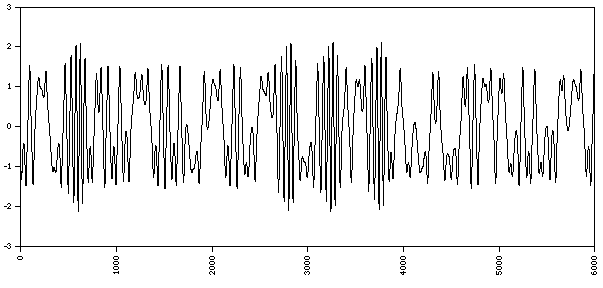 The following 4 diagrams show 2D system for various combinations of a, b, w.
|