Colouring AttractorsWritten by Paul BourkeAttractor data used in the examples is from Dr David Liley and Mathew Dafilis June 1999
The following briefly outlines two methods for colouring chaotic attractors when there is no other convenient attribute from the system that could be mapped to a colour scale. In what follows the following attractor will illustrate the colouring method. Here it is shown with each point a constant colour, namely grey. 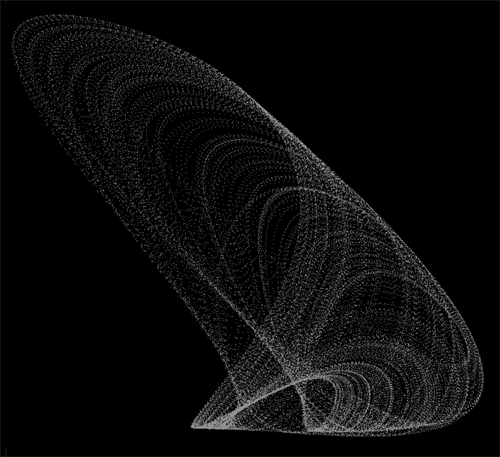
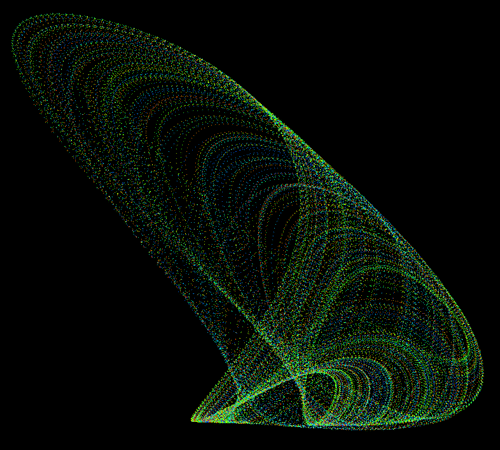
This is often helpful, orbits that are "slow" appear denser as do overlapping regions. In many case such as publication this is the only alternative. One can of course colour an attractor by one of the Cartesian coordinates, this might be helpful when a 3D attractor is being presented in 2D or when a higher dimension attractor is projected into 3D or 2D. Generally one deals with 3D attractors (or at least projections into 3D) and with appropriate use of 3D computer graphics the colouring by one axis doesn't give any additional insight. Due to the very nature of chaotic attractors colouring them by "time" (as the points on the attractor are generated) rarely gives any useful information. On occasion it can give an idea of how fast the points on the attractor diverge but generally it results in a wash of colour, any two tracks are generally a totally different colour. The image below shows our example attractor coloured by time.
A much more useful colouring scheme would use some attribute of the attractor that isn't immediately obvious. There are two canditates, colouring by curvature and colouring by "speed" (the separation between successive points on the attractor). The next image shows our example attractor shaded by curvature, the estimate of the curvature can be made by taking the cross product between the two vectors from the current point to the points a certain distance on either side. 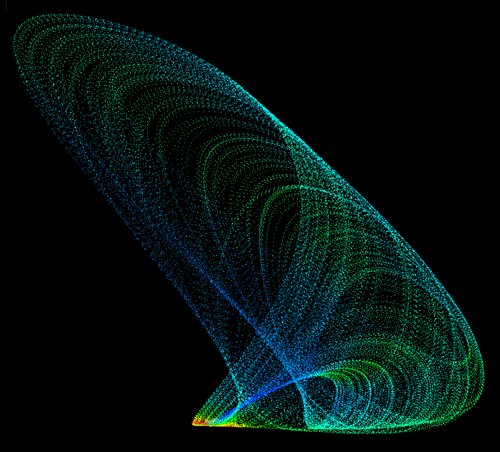
The next image shows the attractor shaded by speed. For this attractor the curvature and speed based colouring visually tells us something about the structure the wasn't obvious before. 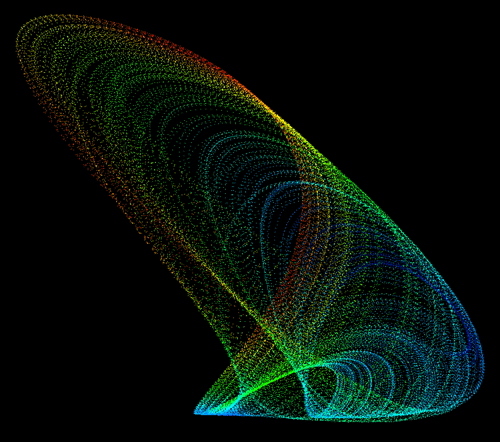 "Solid" attractors created with spheres
In these final examples the points are replaced by small spheres giving the attractor a more solid appearance, the colour is based upon velocity.
Lorenz

|